Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 1 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 3 - Chương 1 - Hình học 9
Lựa chọn câu để xem lời giải nhanh hơn
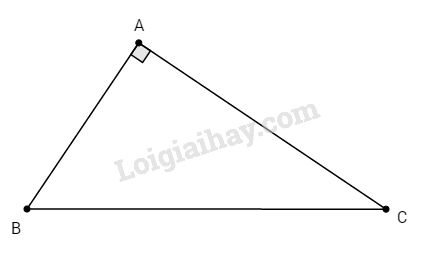
Đề bài Bài 1. Không dùng bảng số và máy tính, hãy sắp xếp các tỉ số lượng giác sau đây theo thứ tự giảm dần : sin25˚; cos35˚; sin50˚; cos70˚. Bài 2. Cho ∆ABC vuông tại A, biết \(\tan B = {3 \over 4}\). Hãy tính các tỉ số lượng giác của góc C. LG bài 1 Phương pháp giải: Sử dụng: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia. Xét góc nhọn, nếu góc tăng thì sin tăng và cosin giảm. Lời giải chi tiết: Ta có: \(\eqalign{ & \cos 35^\circ = \sin \left( {90^\circ - 35^\circ } \right) = \sin 55^\circ \cr & \cos 70^\circ = \sin \left( {90^\circ - 70^\circ } \right) = \sin 20^\circ . \cr} \) Mà \(\sin 55^\circ > \sin 50^\circ > \sin 25^\circ > \sin 20^\circ \) \( \Rightarrow \cos 35^\circ > \sin 50^\circ > \sin 25^\circ \)\(\,> \cos 70^\circ \) LG bài 2 Phương pháp giải: Sử dụng: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia. Cho tam giác ABC có \(\widehat C =\alpha\), ta có: \(\sin \alpha = \dfrac{{cạnh\,đối}}{{cạnh\,huyền}} = \dfrac{{AB}}{{BC}};\)\(\cos \alpha = \dfrac{{cạnh\,kề}}{{cạnh\,huyền}} = \dfrac{{AC}}{{BC}}\) \(\tan \alpha = \dfrac{{cạnh\, đối}}{{cạnh\,kề}} = \dfrac{{AB}}{{AC}};\)\(\cot \alpha = \dfrac{{cạnh\,kề}}{{cạnh\,đối}} = \dfrac{{AC}}{{AB}}\) Lời giải chi tiết:
Ta có: \(\eqalign{ & \tan B = {{AC} \over {AB}} = {3 \over 4} \Rightarrow {{AC} \over 3} = {{AB} \over 4} \cr & \Rightarrow {{A{C^2}} \over 9} = {{A{B^2}} \over {16}} = {{A{C^2} + A{B^2}} \over {9 + 16}}\cr&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {{B{C^2}} \over {25}} \cr & \Rightarrow {{A{C^2}} \over {B{C^2}}} = {9 \over {25}}\,\text{ và }\,{{A{B^2}} \over {B{C^2}}} = {{16} \over {25}} \cr} \) Theo định nghĩa : \(\eqalign{ & \sin B = {{AC} \over {BC}} \cr&\Rightarrow {\sin ^2}B = {{A{C^2}} \over {B{C^2}}} = {9 \over {25}} \cr & \Rightarrow \sin B = {3 \over 5}. \cr} \) Do đó: \(\cos C = {3 \over 5}\) Tương tự: \(\eqalign{ & \cos B = {{AB} \over {BC}} \cr& \Rightarrow {\cos ^2}B = {{A{B^2}} \over {B{C^2}}} = {{16} \over {25}} \cr & \Rightarrow \cos B = {4 \over 5}. \cr} \) Do đó: \(\sin C = {4 \over 5}\) Vì \(\tan B = {3 \over 4} \Rightarrow \cot C = {3 \over 4} \Rightarrow \tan C = {4 \over 3}\) HocTot.Nam.Name.Vn
|