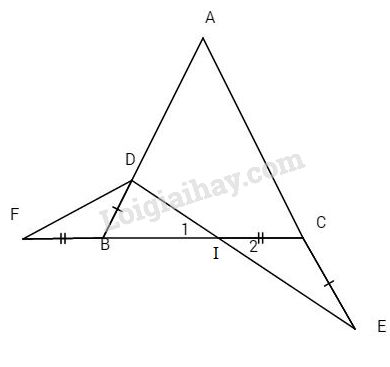
Đề kiểm tra 15 phút - Đề số 5 - Bài 6 - Chương 2 - Hình học 7Giải Đề kiểm tra 15 phút - Đề số 5 - Bài 6 - Chương 2 - Hình học 7 Đề bài Cho tam giác ABC cân tại A. Trên AB lấy D. Trên tia đối của tia CA. Lấy điểm E sao cho CE = BD, DE cắt BC tại I. Trên tia đối của tia BC lấy F sao cho BF = CI. Chứng minh: a) \(\Delta BFD = \Delta CIE\) b) \(\Delta DFI\) cân. c) I là trung điểm của DE. Phương pháp giải - Xem chi tiết Tam giác cân có hai góc ở đáy bằng nhau và hai cạnh bên bằng nhau Hai góc đối đỉnh thì bằng nhau Tính chất hai tam giác bằng nhau Lời giải chi tiết
a) \(\Delta ABC\) cân tại A \( \Rightarrow \widehat B = \widehat C \) \(\Rightarrow \widehat {DBF} = \widehat {ECI}\) (1) (cùng bù với \(\widehat B = \widehat C\)) Xét \(\Delta BFD \) và \( \Delta CIE\) có: +) \(\widehat {DBF} = \widehat {ECI}\) +) \(BD = CE\) (giả thiết) +) \(BF = CI\) (giả thiết). Vậy \(\Delta BFD = \Delta CIE\) (c.g.c). b) Ta có \(\widehat {{I_1}} = \widehat {{I_2}}\) (đối đỉnh), mà \(\widehat {{I_2}} = \widehat F\) (chứng minh trên) \( \Rightarrow \widehat {{I_1}} = \widehat F\) Vậy tam giác DFI cân. c) Tam giác DFI cân (chứng minh trên) \( \Rightarrow FD = ID\). Lại có \(\Delta BFD = \Delta CIE\) (chứng minh trên) \( \Rightarrow FD = IE\). Do đó \(ID = IE\) hay I là trung điểm của DE. HocTot.Nam.Name.Vn
|