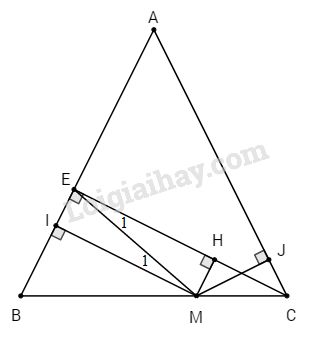
Đề kiểm tra 15 phút - Đề số 8 - Bài 6 - Chương 2 - Hình học 7Giải Đề kiểm tra 15 phút - Đề số 8 - Bài 6 - Chương 2 - Hình học 7 Đề bài Cho tam giác ABC cân tại A, vẽ EC=EH+HC⇒EC=MI+MJ MI⊥AB (E thuộc AB). Lấy M thuộc đoạn BC, vẽ MI⊥AB và MJ⊥AC (I thuộc AB, J thuộc AC). Chứng minh MI+MJ=CE Phương pháp giải - Xem chi tiết Nối M với E, Kẻ MH⊥CE Chứng minh MI=EH và MJ=HC Lời giải chi tiết
Nối M với E. Ta có MI⊥AB (giả thiết); CE⊥AB (giả thiết) ⇒MI//CE. Do đó ^EMI=^MEC (1) (cặp góc so le trong). Kẻ MH⊥CE, Xét hai tam giác vuông MIE và EHM có: +) ME chung +) ^EMI=^MEC ⇒ΔMIE=ΔEHM (g.c.g) ⇒MI=EH (cạnh tương ứng) Mặt khác MH // AB (cùng vuông góc với EC) ⇒^CMH=^CBA=^BCA (2) (cặp góc đồng vị). Xét hai tam giác vuông MHC và CJM có: +) MC chung +) ^CMH=^BCA ⇒ΔMHC=ΔCJM (g.c.g). Do đó MJ=HC, mà EC=EH+HC ⇒EC=MI+MJ. HocTot.Nam.Name.Vn
|