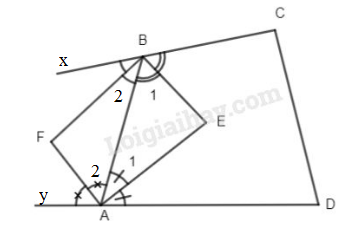
Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 1 - Hình học 8

Đề bài

Cho tứ giác ABCD, phân giác trong của góc A và góc B cắt nhau tại E, phân giác ngoài của góc A và góc B cắt nhau tại F. 

Chứng minh rằng : \(\widehat {AEB} = {{\widehat C + \widehat D} \over 2}\) và \(\widehat {AFB} = {{\widehat A + \widehat B} \over 2}.\)

Lời giải chi tiết

 

Vì BE, AE lần lượt là phân giác góc ABC và góc BAD nên \(\widehat {{B_1}} = \dfrac{{\widehat B}}{2};\widehat {{A_1}} = \dfrac{{\widehat A}}{2}\)

Xét \(\Delta ABE\) có \(\widehat {AEB} = {180^ \circ } - \left( {\widehat {{A_1}} + \widehat {{B_1}}} \right)\) 

Suy ra \(\widehat {AEB} = {180^ \circ } - \left( {{{\widehat A} \over 2} + {{\widehat B} \over 2}} \right)\)

\(= {{{{360}^ \circ } - \left( {\widehat A + \widehat B} \right)} \over 2}\)

Lại có \(\widehat A + \widehat B + \widehat C + \widehat D = {360^ \circ }\) (tổng bốn góc trong tứ giác ABCD)

\( \Rightarrow \widehat C + \widehat D =360^0-( \widehat A + \widehat B )\)

\( \Rightarrow \widehat {AEB} = {{\widehat C + \widehat D} \over 2}\)

Ta có: \(\widehat {{B_2}} = \dfrac{{\widehat {xBA}}}{2};\widehat {{A_2}} = \dfrac{{\widehat {yAB}}}{2}\) (tính chất tia phân giác)

Xét \(\Delta ABF\) có \(\widehat {AFB} = {180^ \circ } - \left( {\widehat {{A_2}} + \widehat {{B_2}}} \right)\) 

\(\begin{array}{l}
= {180^0} - \left( {\dfrac{{\widehat {xBA}}}{2} + \dfrac{{\widehat {yAB}}}{2}} \right)\\
= \dfrac{{{{360}^0} - \left( {\widehat {xBA} + \widehat {yAB}} \right)}}{2}\\
= \dfrac{{{{360}^0} - \left( {{{180}^0} - \widehat B + {{180}^0} - \widehat A} \right)}}{2}\\
= \dfrac{{\widehat A + \widehat B}}{2}
\end{array}\)

Vậy \(  \widehat {AEB} = {{\widehat C + \widehat D} \over 2}\) và \(\widehat {AFB} = {{\widehat A + \widehat B} \over 2}.\)

HocTot.Nam.Name.Vn