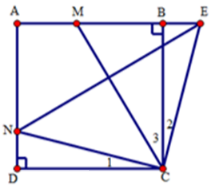
Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 1 - Hình học 8

Đề bài

Cho hình vuông ABCD cạnh bằng a có M và N là hai điểm di động lần lượt trên cạnh AB và AD sao cho $\widehat {MCN} = {45^0}$. Vẽ tia Cx vuông góc với CN,Cx cắt đường thẳng AB tại E.

Chứng minh E là điểm đối xứng của N qua CM.

Lời giải chi tiết

Ta có $CN \bot CE\,\left( {gt} \right)$ mà $\widehat {MCN} = {45^0}$ nên $\widehat {MCE} = {45^0}$ hay $\widehat {{C_2}} + \widehat {{C_3}} = {45^0}$. Mà $\widehat {{C_1}} + \widehat {{C_3}} = {45^0}$ (vì $\widehat {MCN} = {45^0}$) nên $\widehat {{C_1}} = \widehat {{C_2}}$. 

Xét tam giác CDN và tam giác CBE có:

BC = DC  (do ABCD là hình vuông); $\widehat D = \widehat B = {90^0}$ ; $\widehat {{C_1}} = \widehat {{C_2}}$ (cmt)

Suy ra $\Delta CDN = \Delta CBE(g.c.g)$ .Suy ra $CN = CE$

Xét tam giác $CEN$ có $CN = CE$ (cmt) nên tam giác $CEN$ là tam giác cân tại $C.$

Suy ra phân giác $CM$ đồng thời là đường trung trực của $NE .$ 

Vậy E là điểm đối xứng của N qua CM.

HocTot.Nam.Name.Vn