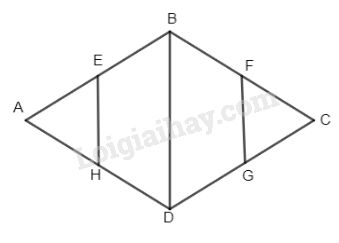
Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 2 - Hình học 8

Đề bài

Cho hình thoi ABCD có $\widehat A = {60^ \circ }$. Gọi E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Chứng minh rằng EBFGDH  là lục giác đều.

Lời giải chi tiết

$\Delta ABD$ cân (AB = AD) có $\widehat A = {60^ \circ }$ (gt) nên $\Delta ABD$ đều

$\Rightarrow AB = BC = CD = AD = BD$ và EH, FG lần lượt là các đường trung bình của $\Delta ABD$ và $\Delta CBD.$

Ta có: $EH = FG = \dfrac{1 }{2}BD$

Lại có E, F, G, H là các trung điểm của AB, BC, CD, DE nên EB = BF = FG = GD = DH = HE (1)

Mặt khác $\widehat {AEH} = {60^ \circ }(\Delta AEH (đều)$ $\Rightarrow \widehat {BEH} = {120^ \circ }$ (kề bù)

Tương tự ta chứng minh được $\widehat {BFG} = \widehat {DGF} = \widehat {DHE} = {120^ \circ }$

Hiển nhiên $\widehat {ABC} = \widehat {ADC} = {120^ \circ }$ (vì $\widehat A = {60^ \circ }$)

$\Rightarrow \widehat {BFG} = \widehat {DGF} = \widehat {HDE} = \widehat {EBF}$$\, = \widehat {HDG} = {120^ \circ }$   (2)

Từ (1) và (2) $\Rightarrow EBFGDH$ là lục giác đều.

HocTot.Nam.Name.Vn