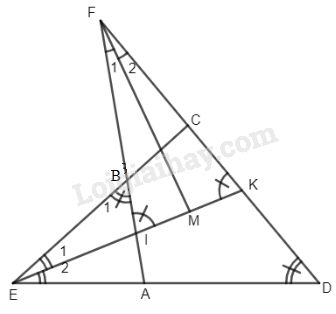
Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 4 - Bài 1 - Chương 1 - Hình học 8 Đề bài Tứ giác ABCD có các góc đối bù nhau. Các cạnh AD và BC cắt nhau tại E ; AB và DC cắt nhau tại F. Phân giác của hai góc CED và AFD cắt nhau tại M. Chứng minh rằng \(FM \bot EM.\) Phương pháp giải - Xem chi tiết Sử dụng: Trong một tam giác, góc ngoài tại 1 đỉnh bằng tổng hai góc trong không kề với đỉnh đó. Trong tam giác cân, đường phân giác của góc ở đỉnh cũng là đường cao của tam giác. Lời giải chi tiết Gọi I, K lần lượt là giao điểm của EM với AB và DC. Ta có : \(\widehat {FIK} = \widehat {{E_1}} + \widehat {{D_1}}\) (góc ngoài của \(\Delta EIB\)) \(\widehat {FKI} = \widehat {{E_2}} + \widehat D\)(góc ngoài của \(\Delta EKD\) ) Mà \(\widehat {{E_1}} = \widehat {{E_2}}\) (giả thiết) \(\widehat {{B_1}} = \widehat D\) (cùng bù với \(\widehat {ABC}\) ) \( \Rightarrow \widehat {FIK}\) cân tại F. Trong tam giác cân FIK có FM là phân giác nên FM cũng là đường cao. Suy ra \(FM \bot IK\) hay \(FM \bot EM.\)
HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
