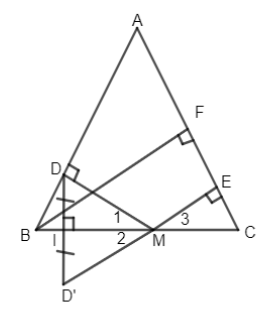
Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 6 - Chương 1 - Hình học 8 GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn Đề bài Cho tam giác ABC cân tại A. Lấy M bất kì thuộc cạnh BC, kẻ MD⊥AB,ME⊥AC. Gọi D′ là điểm đối xứng của D qua BC. a) Chứng minh ba điểm E, M, D′ thẳng hàng. b) Kẻ BF⊥AC. Chứng minh ED′=BF. Phương pháp giải - Xem chi tiết +) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng dd nếu dd là đường trung trực của đoạn thẳng nối hai điểm đó. +) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó. +) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy cũng là đường trung trực, đường phân giác. Lời giải chi tiết
a) D' đối xứng với D qua BC ⇒DD′⊥BC và ID′=ID (I là giao điểm của DD′ và BC Suy ra tam giác MDD' có MI vừa là đường trung tuyến vừa là đường cao ⇒ΔDMD′ cân tại M, do đó đường cao MI đồng thời là phân giác: ^M1=^M2 , mà ^M1=^M3 (cùng phụ với ˆB=ˆC ) ⇒^M2=^M3 mà ^M3+^EMB=180∘ ⇒^M2+^EMB=180∘ chứng tỏ E,M,D′ thẳng hàng. b) Vì tam giác MDD' cân tại M nên MD=MD′ Xét ΔBDM và ΔBD′M có: MD=MD′ (cmt) ^M1=^M2 (cmt) Cạnh MB chung Suy ra ΔBDM=ΔBD′M(c.g.c) ⇒^BD′M=^BDM=90∘ hay D′B⊥D′E⇒D′B//EF. Lại có BF//D′E(⊥AC) nên BFED′ là hình thang có hai cạnh bên song song ⇒ED′=BF. HocTot.Nam.Name.Vn
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
|