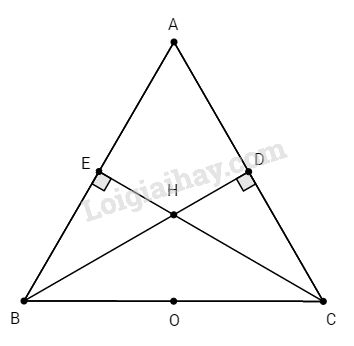
Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 2 - Hình học 9Giải Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 2 - Hình học 9 Đề bài Cho ∆ABC đều có cạnh bằng a, các đường cao BD và CE cắt nhau tại H. a. Chứng minh rằng bốn điểm B, E, D, C thuộc cùng một đường tròn. Hãy xác định tâm bán kính của đường tròn đó. b. Chứng minh rằng điểm H nằm trong đường tròn và điểm A nằm ngoài đường tròn đi qua bốn điểm B, E, D, C. Phương pháp giải - Xem chi tiết Sử dụng: a) Để chứng minh 4 điểm cùng thuộc một đường tròn, ta chứng minh 4 điểm đó cùng cách đều một điểm cố định b) Nếu A nằm trên đường tròn (O;R) thì OA=R Nếu A nằm trong đường tròn (O; R) thì OA<R Nếu A nằm ngoài đường tròn (O;R) thì OA>R. Lời giải chi tiết
a. Gọi O là trung điểm của BC, các tam giác vuông BDC và BEC có OD, OE là các đường trung tuyến thuộc cạnh huyền BC nên \(\eqalign{ & OD = OE = {1 \over 2}BC \cr & hay\,OD = OE = OB = OC = {1 \over 2}a \cr} \) Vậy bốn điểm B, E, D, C thuộc cùng một đường tròn, tâm O là trung điểm của BC và bán kính bằng \({1 \over 2}BC = {1 \over 2}a\) b. ∆ABC đều nên trực tâm H cũng đồng thời là trọng tâm, AO là trung tuyến nên đồng thời là đường cao và A, H, O thẳng hàng. Xét tam giác vuông AOB, ta có: \(AO = \sqrt {A{B^2} - O{B^2}} \) (định lí Pi-ta-go ) \( = \sqrt {{a^2} - {{\left( {{a \over 2}} \right)}^2}} = \sqrt {{{3{a^2}} \over 4}} = {{a\sqrt 3 } \over 2}\) Mặt khác, vì H là trọng tâm của ∆ABC nên: \(OH = {1 \over 3}AO = {1 \over 3}.{{a\sqrt 3 } \over 2} = {{a\sqrt 3 } \over 6}\) Nhận thấy: \({{a\sqrt 3 } \over 6} < {a \over 2},\) do đó điểm H nằm trong đường tròn \(\left( {O,{a \over 2}} \right);\) Và \({{a\sqrt 3 } \over 2} > {a \over 2},\) do đó điểm A nằm ngoài đường tròn \(\left( {O;{a \over 2}} \right).\) HocTot.Nam.Name.Vn
|