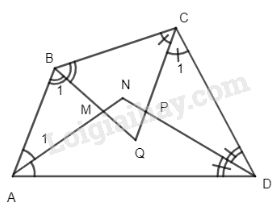
Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 1 - Hình học 8

Đề bài

Các đường phân giác trong của tứ giác ABCD tạo thành một tứ giác. Chứng minh rằng tứ giác đó có các góc đối bù nhau.

Lời giải chi tiết

Gọi MNPQ là tứ giác được tạo thành.

Xét tứ giác ABCD, ta có :

$\widehat A + \widehat B + \widehat C + \widehat D = {360^ \circ }$ (tổng bốn góc trong tứ giác bằng $360^0$)

$\Rightarrow {{\widehat A} \over 2} + {{\widehat B} \over 2} + {{\widehat C} \over 2} + {{\widehat D} \over 2} = {180^ \circ }.$

Xét $\Delta AMB$ có $\widehat {{A_1}} + \widehat {AMB} + \widehat {{B_1}} = {180^ \circ }$

Hay ${{\widehat A} \over 2} + \widehat {AMB} + {{\widehat B} \over 2} = {180^ \circ }.$

Tương tự với $\Delta CPD:{{\widehat C} \over 2} + \widehat {CPD} + {{\widehat D} \over 2} = {180^ \circ }.$

$\Rightarrow {{\widehat A} \over 2} + \widehat {AMB} + {{\widehat B} \over 2}$$+{{\widehat C} \over 2} + \widehat {CPD} + {{\widehat D} \over 2}=180^0+180^0$

$\Rightarrow \widehat {AMB} + \widehat {CPD}$$+{{\widehat A} \over 2} + {{\widehat B} \over 2} + {{\widehat C} \over 2} + {{\widehat D} \over 2}=360^0$

$\Rightarrow \widehat {AMB} + \widehat {CPD} = {180^ \circ }$

$\Rightarrow \widehat {NMQ} + \widehat {NPQ} = {180^ \circ }$

$\Rightarrow \widehat {MNP} + \widehat {MQP}$$\,= {360^ \circ } - \left( {\widehat {NMQ} + \widehat {NPQ}} \right)$$\, = {360^ \circ } - {180^ \circ } = {180^ \circ }.$

Vậy tứ giác MNPQ có các góc đối bù nhau.

HocTot.Nam.Name.Vn