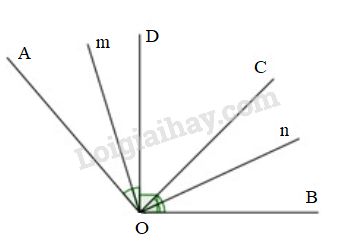
Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 1 - Hình học 7Giải Đề kiểm tra 15 phút - Đề số 2 - Bài 2 - Chương 1 - Hình học 7 Đề bài Cho góc ^AOB=120o, vẽ các tia OC và OD nằm trong góc AOB sao cho OC⊥OA và OD⊥OB a) Tính góc ^COD. b) Gọi Om, On lần lượt là hai tia phân giác của hai góc ^AOD và ^BOC. Chứng minh rằng Om⊥On. Phương pháp giải - Xem chi tiết Sử dụng: Công thức cộng góc: Nếu tia Oz nằm giữa hai tia Ox và Oy thì ^xOz+^yOz=^xOy Tính chất tia phân giác của 1 góc. Lời giải chi tiết
a) Ta có OC⊥OA nên ^OAC=90o. Tia OC nằm giữa hai tia OA và OB nên ^AOC+^COB=^AOB Hay 90o+^COB=120o⇒^COB=30o. Chứng minh tương tự ta có ^AOD=30o. Do đó ^DOC=^AOB−(^AOD+^COB) =120o−(30o+30o)=60o. b) Om là tia phân giác của ^AOD nên ^AOm=^DOm=^AOD2=15o. Tương tự On là phân giác của ^BOC nên ^BOn=^COn=^COB2=15o. ⇒^mOn=^DOm+^DOC+^COn=15o+60o+150=90o, Chứng tỏ Om⊥On. HocTot.Nam.Name.Vn
|