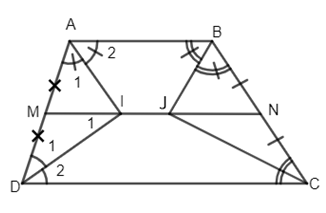
Đề kiểm tra 15 phút - Đề số 10 - Bài 4, 5 - Chương 1 - Hình học 8Giải Đề kiểm tra 15 phút - Đề số 10 - Bài 4, 5 - Chương 1 - Hình học 8 Đề bài Cho hình thang ABCD \(\left( {AB//CD} \right)\). Các tia phân giác của các góc A và D cắt nhau tại I, và của các góc B và C cắt nhau tại J. Gọi M và N lần lượt là trung điểm của AD và BC. Chứng minh rằng: bốn điểm M, N, I, J thẳng hàng. Phương pháp giải - Xem chi tiết Sử dụng: - Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. - Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy. - Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền. Lời giải chi tiết
Vì AI và DI lần lượt là tia phân giác của góc A và góc D nên \(\widehat {{A_1}} = \dfrac{{\widehat A}}{2};\widehat {{D_1}} = \dfrac{{\widehat D}}{2}\) Vì AB//CD nên \(\widehat A + \widehat D = {180^ \circ }\) (cặp góc trong cùng phía) \( \Rightarrow \dfrac{{\widehat A} }{ 2} + \dfrac{{\widehat D}}{2} = {90^ \circ }\) \(\Rightarrow \widehat {{A_1}} + \widehat {{D_1}} = {90^ \circ }\) Xét tam giác AID có \( \widehat {AID}=180^0-(\widehat {{A_1}} + \widehat {{D_1}})\)\(=180^0-90^0 = {90^ \circ }\) Lại có M là trung điểm của AD (gt) nên MI là trung tuyến của tam giác vuông AID nên MI = MD hay \(\Delta DMI\) cân tại M \( \Rightarrow \widehat {{D_1}} = \widehat {{I_1}}\) Mà \(\widehat {{D_1}} = \widehat {{D_2}}\left( {gt} \right) \Rightarrow \widehat {{D_2}} = \widehat {{I_1}}\) Do đó \(MI// DC.\) Vì M và N lần lượt là trung điểm của AD và BC nên MN là đường trung bình của hình thang ABCD, do đó \(MN// DC.\) Vậy MI và MN phải trùng nhau (Tiên đề Ơ clit) hay ba điểm M, I, N thẳng hàng. Chứng minh tương tự ta được M, J, N thẳng hàng. Vậy bốn điểm M, I, J, N thẳng hàng. HocTot.Nam.Name.Vn
|