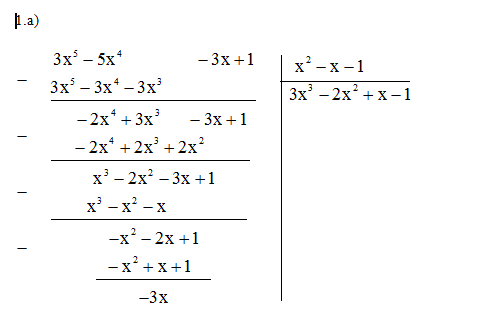Đề kiểm tra 15 phút - Đề số 1 - Bài 12 - Chương 1 - Đại số 8Giải Đề kiểm tra 15 phút - Đề số 1 - Bài 12 - Chương 1 - Đại số 8 Đề bài Làm tính chia: a) \(\left( {3{x^5} - 5{x^4} - 3x + 1} \right):\left( {{x^2} - x - 1} \right)\) b) \(\left( {{x^4} - 1} \right):\left( {x - 1} \right)\) Phương pháp giải - Xem chi tiết a) Đặt phép tính chia b) Phân tích \(x^4-1\) thành nhân tử rồi chia. Lời giải chi tiết
Vậy \(3{x^5} - 5{x^4} - 3x + 1 \)\(\;= \left( {{x^2} - x - 1} \right)\left( {3{x^3} - 2{x^2} + x - 1} \right) - 3x.\) b) Ta có: \({x^4} - 1 = \left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right) \)\(\;= \left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right)\) Vậy \(\left( {{x^4} - 1} \right):\left( {x - 1} \right)\) \(= \left( {x - 1} \right)\left( {x + 1} \right)\left( {{x^2} + 1} \right):\left( {x - 1} \right)\)\(=\left( {x + 1} \right)\left( {{x^2} + 1} \right) = {x^3} + {x^2} + x + 1.\) HocTot.Nam.Name.Vn
|