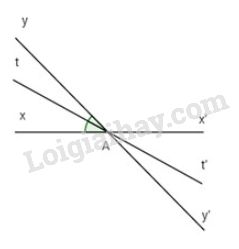
Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 1 - Hình học 7

Đề bài

Hai đường thẳng xx’ và yy’ cắt nhau tại A, biết $\widehat {xAy} = {36^o}.$

a) Tính các góc $\widehat {yAx'},\widehat {x'Ay'}$ và $\widehat {y'Ax}.$

b) Vẽ tia phân giác At của $\widehat {xAy}$ và tia phân giác của $\widehat {x'Ay'}.$ Chứng tỏ rằng hai tia At và At’ là hai tia đối nhau.

Lời giải chi tiết

a) $\widehat {xAy} + \widehat {yAx'} = {180^o}$ (kề bù)

${36^o} + \widehat {yAx'} = {180^o}$

$\widehat {yAx'} = {180^o} - {36^o}$ 

$\widehat {yAx'} = {144^o}$

$\widehat {x'Ay'} = \widehat {xAy} = {36^o}$(đối đỉnh)

$\widehat {y'Ax} = \widehat {yAx'} = {144^o}$(đối đỉnh)

b) At là phân giác của $\widehat {xAy}$ nên $\widehat {xAt} = \widehat {yAt} = \dfrac{{\widehat {xAy}}}{ 2} =\dfrac {{{{36}^0}} }{ 2} = {18^o}.$

$\widehat {x'Ay'} = \widehat {xAy} = {36^o}$ (đối đỉnh), At’ là tia phân giác của $\widehat {x'Ay'}$ nên $\widehat {x'At'} = \widehat {y'At'} = \dfrac{{\widehat {x'Ay'}}}{ 2} = \dfrac{{{{36}^o}}}{ 2} = {18^o}.$

$\Rightarrow \widehat {xAt} + \widehat {xAy'} + \widehat {y'At'}$$= 18^0+144^0+18^0=180^0$

Chứng tỏ At’ và At là hai tia đối nhau.

HocTot.Nam.Name.Vn