Nội dung từ Loigiaihay.Com
Câu hỏi:
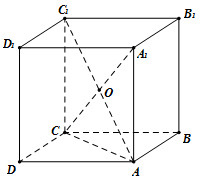
Cho hình lập phương \(ABCD.{A_1}{B_1}{C_1}{D_1}\). Gọi \(O\) là tâm của hình lập phương. Chọn đẳng thức đúng?
- A \(\overrightarrow {AO} = \dfrac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right).\)
- B \(\overrightarrow {AO} = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right).\)
- C \(\overrightarrow {AO} = \dfrac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right).\)
- D \(\overrightarrow {AO} = \dfrac{2}{3}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right).\)
Phương pháp giải:
Sử dụng công thức ba điểm và công thức hình bình hành.
Lời giải chi tiết:
Do \(ABCD.{A_1}{B_1}{C_1}{D_1}\) là hình lập phương nên \(AC{C_1}{A_1}\) là hình chữ nhật.
\( \Rightarrow O\) là trung điểm của \(A{C_1} \Rightarrow \overrightarrow {AO} = \dfrac{1}{2}\overrightarrow {A{C_1}} \).
Ta có: \(\overrightarrow {A{C_1}} = \overrightarrow {A{A_1}} + \overrightarrow {AC} = \overrightarrow {A{A_1}} + \overrightarrow {AB} + \overrightarrow {AD} \)
\( \Rightarrow \overrightarrow {AO} = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {A{A_1}} } \right).\)
Chọn B.













