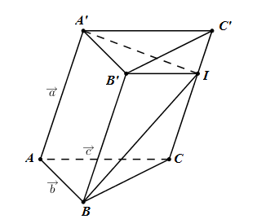
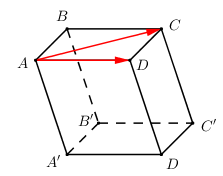
Phương pháp giải:

Sử dụng công thức trung điểm

Lời giải chi tiết:

Mệnh đề sai là: \(I\) là trung điểm \(AB\) thì \(\overrightarrow {MI\,\,}  = \overrightarrow {MA\,\,}  + \overrightarrow {MB\,\,} \)với mọi điểm \(M\).

Sửa lại: \(I\) là trung điểm \(AB\) thì \(2\overrightarrow {MI\,\,}  = \overrightarrow {MA\,\,}  + \overrightarrow {MB\,\,} \)với mọi điểm \(M\).

Chọn: B

Phương pháp giải:

Sử dụng công thức ba điểm.

Lời giải chi tiết:

\(\begin{array}{l}\overrightarrow {GB}  + \overrightarrow {GA'}  + \overrightarrow {GB'}  + \overrightarrow {GC'}  = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {GI}  + \overrightarrow {IB}  + \overrightarrow {GI}  + \overrightarrow {IA'}  + \overrightarrow {GI}  + \overrightarrow {IB'}  + \overrightarrow {GI}  + \overrightarrow {IC'}  = \overrightarrow 0 \\ \Leftrightarrow 4\overrightarrow {GI}  + \left( {\overrightarrow {IB}  + \overrightarrow {IA'}  + \overrightarrow {IB'}  + \overrightarrow {IC'} } \right) = \overrightarrow 0 \\ \Leftrightarrow \overrightarrow {IG}  = \dfrac{1}{4}\left( {\overrightarrow {IC}  + \overrightarrow {CA}  + \overrightarrow {AB}  + \overrightarrow {IC'}  + \overrightarrow {C'A'}  + \overrightarrow {IC'}  + \overrightarrow {C'A'}  + \overrightarrow {A'B'}  + \overrightarrow {IC'} } \right)\\ \Leftrightarrow \overrightarrow {IG}  = \dfrac{1}{4}\left( {\overrightarrow {IC}  + 3\overrightarrow {IC'}  + 3\overrightarrow {CA}  + 2\overrightarrow {A'B'} } \right)\\ \Leftrightarrow \overrightarrow {IG}  = \dfrac{1}{4}\left( { - \dfrac{2}{3}\overrightarrow a  + \overrightarrow a  - 3\overrightarrow c  + 2\overrightarrow b } \right) = \dfrac{1}{4}\left( {\dfrac{1}{3}\overrightarrow a  + 2\overrightarrow b  - 3\overrightarrow c } \right)\end{array}\)

Chọn A.

Phương pháp giải:

Sử dụng quy tắc hình bình hành: Cho hình bình hành \(ABCD\) ta có: \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} .\)

Lời giải chi tiết:

Ta có: \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = \left( {\overrightarrow {AB}  + \overrightarrow {AD} } \right) + \overrightarrow {AC}  = 2\overrightarrow {AC} .\)

Chọn  B.         

Phương pháp giải:

Sử dụng công thức ba điểm và các vectơ bằng nhau.

Lời giải chi tiết:

Ta có: \(\overrightarrow {AC'}  = \overrightarrow {AB}  + \overrightarrow {BC}  + \overrightarrow {CC'} \).

Mà \(\overrightarrow {BC}  = \overrightarrow {AD} ,\,\,\overrightarrow {CC'}  = \overrightarrow {AA'}  \Rightarrow \overrightarrow {AC'}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'} \).

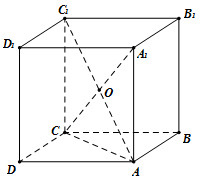
Chọn C.

Phương pháp giải:

Sử dụng công thức \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \widehat {\left( {\overrightarrow a ;\overrightarrow b } \right)}\). Đặc biệt khi \(\overrightarrow a  \bot \overrightarrow b  \Rightarrow \overrightarrow a .\overrightarrow b  = 0\).

Lời giải chi tiết:

Ta có \(\left\{ \begin{array}{l}AB//A'B'\\A'B' \bot A'D'\end{array} \right. \Rightarrow AB \bot A'D' \Rightarrow \overrightarrow {AB} .\overrightarrow {A'D'}  = 0\).

Chọn C.

Phương pháp giải:

Sử dụng công thức ba điểm và công thức hình bình hành.

Lời giải chi tiết:

Do \(ABCD.{A_1}{B_1}{C_1}{D_1}\) là hình lập phương nên \(AC{C_1}{A_1}\) là hình chữ nhật.

\( \Rightarrow O\) là trung điểm của \(A{C_1} \Rightarrow \overrightarrow {AO}  = \dfrac{1}{2}\overrightarrow {A{C_1}} \).

Ta có: \(\overrightarrow {A{C_1}}  = \overrightarrow {A{A_1}}  + \overrightarrow {AC}  = \overrightarrow {A{A_1}}  + \overrightarrow {AB}  + \overrightarrow {AD} \)

 \( \Rightarrow \overrightarrow {AO}  = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {A{A_1}} } \right).\)

Chọn B.

Phương pháp giải:

\(\angle \left( {\overrightarrow a ;\overrightarrow b } \right) = \angle \left( {\overrightarrow a ;\overrightarrow c } \right)\) với \(\overrightarrow c \) là vectơ cùng hướng với \(\overrightarrow b \).

Lời giải chi tiết:

Ta có : \(\overrightarrow {AD} \) cùng hướng với \(\overrightarrow {B'C'} \)

\( \Rightarrow \angle \left( {\overrightarrow {B'C'} ;\overrightarrow {AC} } \right) = \angle \left( {\overrightarrow {AD} ;\overrightarrow {AC} } \right) = \angle DAC\).

Chọn B.

Phương pháp giải:

Sử dụng công thức ba điểm.

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = \overrightarrow {AG}  + \overrightarrow {GB}  + \overrightarrow {AG}  + \overrightarrow {GC}  + \overrightarrow {AG}  + \overrightarrow {GD} \\ = 3\overrightarrow {AG}  + \left( {\overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD} } \right) = 3\overrightarrow {AG}  - \overrightarrow {GA}  = 4\overrightarrow {AG} \\ \Rightarrow \overrightarrow {AG}  = \dfrac{1}{4}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right)\end{array}\)

Chọn D.

Phương pháp giải:

Sử dụng công thức \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right) = \dfrac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).

Lời giải chi tiết:

Đặt \(AD = x \Rightarrow AC = \dfrac{3}{2}x,\,\,CD = x\).

Ta có:

\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {CD}  = \overrightarrow {AB} \left( {\overrightarrow {AD}  - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD}  - \overrightarrow {AB} .\overrightarrow {AC} \\ = AB.AD.\cos \angle DAB - AB.AC.\cos \angle CAB\\ = AB.x.\cos {60^0} - AB.\dfrac{3}{2}x.\cos {60^0}\\ = AB.x.\dfrac{1}{2} - AB.\dfrac{3}{2}x.\dfrac{1}{2} =  - \dfrac{1}{4}AB.x\end{array}\)

Khi đó ta có \(\cos \left( {\overrightarrow {AB} ;\overrightarrow {CD} } \right) = \dfrac{{\overrightarrow {AB} .\overrightarrow {CD} }}{{AB.CD}} = \dfrac{{ - \dfrac{1}{4}AB.x}}{{AB.x}} =  - \dfrac{1}{4} < 0\).

Vậy \(\cos \left( {AB;CD} \right) = \dfrac{1}{4} \Rightarrow \cos \varphi  = \dfrac{1}{4}\).

Chọn A.

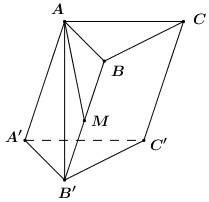
Phương pháp giải:

Hình hộp là hình lăng trụ có đáy là hình bình hành.

Lời giải chi tiết:

Do \(ABC'D'\) là hình bình hành \( \Rightarrow \left\{ \begin{array}{l}AB = CD\\AB \nearrow  \nearrow D'C'\end{array} \right. \Rightarrow \overrightarrow {AB}  = \overrightarrow {D'C'} \).

Chọn B.

Phương pháp giải:

Sử dụng công thức ba điểm.

Lời giải chi tiết:

Ta có

\(\begin{array}{l}\overrightarrow {AM}  = \overrightarrow {AB}  + \overrightarrow {BM}  = \overrightarrow {AC}  - \overrightarrow {BC}  + \dfrac{1}{2}\overrightarrow {BB'} \\ =  - \overrightarrow {CA}  + \overrightarrow {CB}  + \dfrac{1}{2}\overrightarrow {AA'}  =  - \overrightarrow a  + \overrightarrow b  + \dfrac{1}{2}\overrightarrow c \end{array}\)

Chọn B.

Phương pháp giải:

Sử dụng công thức: \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \) với \(G\) là trọng tâm \(\Delta ABC\).

Lời giải chi tiết:

Do \(G\) là trọng tâm \(\Delta ABC\) nên \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

\(\begin{array}{l} \Leftrightarrow \overrightarrow {GD}  + \overrightarrow {DA}  + \overrightarrow {GB}  + \overrightarrow {DB}  + \overrightarrow {GD}  + \overrightarrow {DC}  = \overrightarrow 0 \\ \Leftrightarrow 3\overrightarrow {GD}  + \left( {\overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC} } \right) = \overrightarrow 0  \Leftrightarrow \overrightarrow {DA}  + \overrightarrow {DB}  + \overrightarrow {DC}  = 3\overrightarrow {DG} \end{array}\)

Vậy mệnh đề C đúng.

Chọn C.

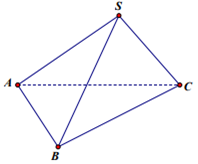
Phương pháp giải:

+) \(I\) là trung điểm của \(MN \Rightarrow \overrightarrow {IM}  + \overrightarrow {IN}  = \overrightarrow 0 \) và \(\overrightarrow {AM}  + \overrightarrow {AN}  = 2\overrightarrow {AI} \,\,\forall A\).

+) Hai vectơ \(\overrightarrow a ,\,\,\overrightarrow b \) được gọi là cùng phương nếu tồn tại hằng số \(k \ne 0\) sao cho \(\overrightarrow a  = k\overrightarrow b \).

Lời giải chi tiết:

Do \(\overrightarrow {MN} \) và \(\overrightarrow {NI} \) là 2 vectơ ngược hướng nên đáp án B sai.

Chọn B

Phương pháp giải:

Sử dụng công thức: \(\overrightarrow {MA}  + \overrightarrow {MB}  = 2\overrightarrow {MI} \,\,\forall M\), với \(I\) là trung điểm của \(AB\).

Lời giải chi tiết:

Do \(O\) là trung điểm của \(AC,\,\,BD \Rightarrow \left\{ \begin{array}{l}\overrightarrow {SA}  + \overrightarrow {SC}  = 2\overrightarrow {SO} \\\overrightarrow {SB}  + \overrightarrow {SD}  = 2\overrightarrow {SO} \end{array} \right. \Rightarrow \) Mệnh đề A, B đúng.

\( \Rightarrow \overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD}  = 2\overrightarrow {SO}  \Rightarrow \) Mệnh đề C đúng.

Chọn D

Phương pháp giải:

\(d \bot d' \Rightarrow \overrightarrow u  \bot \overrightarrow {u'} \).

Lời giải chi tiết:

\(d \bot d' \Rightarrow \overrightarrow u  \bot \overrightarrow {u'}  \Rightarrow \left( {\overrightarrow u ;\overrightarrow {u'} } \right) = {90^0} \Rightarrow \cos \left( {\overrightarrow u ;\overrightarrow {u'} } \right) = \cos {90^0} = 0\).

Chọn D

Phương pháp giải:

Cho 3 vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \), trong đó \(\overrightarrow a ,\,\,\overrightarrow b \) không cùng phương. Điều kiện cần và đủ để ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) đồng phẳng là tồn tại cặp số \(\left( {m;n} \right)\) sao cho \(\overrightarrow c  = m\overrightarrow a  + n\overrightarrow b \).

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}2\overrightarrow y  - \overrightarrow x  = 2\left( {\overrightarrow a  - \overrightarrow b  - \overrightarrow c } \right) - \left( {2\overrightarrow a  + \overrightarrow b } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =  - 3\overrightarrow b  - 2\overrightarrow c  = \overrightarrow z \end{array}\)

Do đó ba vectơ \(\overrightarrow x ,\,\,\overrightarrow y ,\,\,\overrightarrow z \) đồng phẳng.

Chọn A

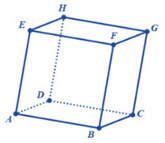
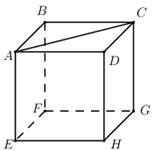
Phương pháp giải:

Sử dụng công thức ba điểm \(\overrightarrow {AB}  = \overrightarrow {AM}  + \overrightarrow {MB} \,\,\forall M\).

Lời giải chi tiết:

Ta có \(\overrightarrow {MP}  = \overrightarrow {MA}  + \overrightarrow {AP}  = \overrightarrow {MA}  - m\overrightarrow {PD} \).

Chọn A.

Phương pháp giải:

Sử dụng công thức hình bình hành.

Lời giải chi tiết:

\(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AE}  = \overrightarrow {AC}  + \overrightarrow {AE}  = \overrightarrow {AG} \).

Chọn A.

Phương pháp giải:

Lời giải chi tiết:

\(\angle \left( {\overrightarrow {AC} ;\overrightarrow {FG} } \right) = \angle \left( {\overrightarrow {BC} ;\overrightarrow {AC} } \right) = {45^0}\).

Chọn A.

Phương pháp giải:

Sử dụng công thức \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \angle \left( {\overrightarrow a ;\overrightarrow b } \right)\).

Lời giải chi tiết:

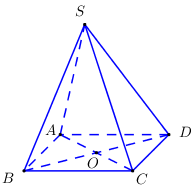
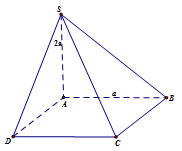
Ta có:

\(\begin{array}{l}\overrightarrow {AB} .\overrightarrow {A'C'}  = AB.A'C'.\cos \angle \left( {\overrightarrow {AB} ;\overrightarrow {A'C'} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = AB.A'C'.\cos \angle \left( {\overrightarrow {A'B'} ;\overrightarrow {A'C'} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = a.a\sqrt 2 .\cos {45^0} = {a^2}\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = {a^2}\end{array}\)

Chọn C.

Phương pháp giải:

Áp dụng quy tắc hình hình hành.

Lời giải chi tiết:

Ta có \(ABCD\) là hình vuông \( \Rightarrow \overrightarrow {AC}  = \overrightarrow {AB}  + \overrightarrow {AD}  \Rightarrow \left\{ \begin{array}{l}m = 1\\n = 1\\p = 0\end{array} \right. \Rightarrow m + n + p = 1 + 1 + 0 = 2\).

Chọn B.

Phương pháp giải:

Sử dụng công thức ba điểm: \(\overrightarrow {AB}  = \overrightarrow {AM}  + \overrightarrow {MB} \) và công thức trọng tâm của tam giác: \(\overrightarrow {MG}  = \frac{1}{3}\left( {\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC} } \right)\) với \(G\) là trọng tâm tam giác \(ABC\), \(M\) là điểm bất kì.

Lời giải chi tiết:

\(\begin{array}{l}\overrightarrow {MG}  = \overrightarrow {MS}  + \overrightarrow {SG}  =  - \dfrac{1}{3}\overrightarrow {SA}  + \dfrac{1}{3}\left( {\overrightarrow {SA}  + \overrightarrow {SB}  + \overrightarrow {SC} } \right)\\ =  - \dfrac{1}{3}\overrightarrow {SA}  + \dfrac{1}{3}\overrightarrow {SA}  + \dfrac{1}{3}\overrightarrow {SB}  + \dfrac{1}{3}\overrightarrow {SC}  = \dfrac{1}{3}\overrightarrow {SB}  + \dfrac{1}{3}\overrightarrow {SC} \end{array}\)

Chọn B.

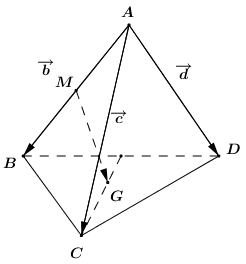
Phương pháp giải:

Sử dụng khái niệm đồng phẳng của vectơ.

Lời giải chi tiết:

Trong không gian, ba vectơ \(\overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c \) được gọi là đồng phẳng nếu và chỉ nếu chúng có giá song song với một mặt phẳng nào đó.

Chọn D.

Phương pháp giải:

Sử dụng công thức trọng tâm: Cho tam giác \(BCD\) có trọng tâm \(G\). Với mọi điểm \(M\) ta luôn có: \(\overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = 3\overrightarrow {MG} \).

Lời giải chi tiết:

Vì \(G\) là trọng tâm tam giác \(BCD\) nên ta có:

\(\begin{array}{l}\,\,\,\,\,\,\overrightarrow {MG}  = \dfrac{1}{3}\left( {\overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD} } \right)\\ \Leftrightarrow \overrightarrow {MG}  = \dfrac{1}{3}\left( {\dfrac{1}{2}\overrightarrow {AB}  - \overrightarrow {CM}  - \overrightarrow {DM} } \right)\\ \Leftrightarrow \overrightarrow {MG}  = \dfrac{1}{6}\overrightarrow b  - \dfrac{1}{3}.\dfrac{1}{2}\left( {\overrightarrow {CA}  + \overrightarrow {CB} } \right) - \dfrac{1}{3}.\dfrac{1}{2}\left( {\overrightarrow {DA}  + \overrightarrow {DB} } \right)\\ \Leftrightarrow \overrightarrow {MG}  = \dfrac{1}{6}\overrightarrow b  - \dfrac{1}{6}\left( {\overrightarrow {CA}  + \overrightarrow {CA}  + \overrightarrow {AB} } \right) - \dfrac{1}{6}\left( {\overrightarrow {DA}  + \overrightarrow {DA}  + \overrightarrow {AB} } \right)\\ \Leftrightarrow \overrightarrow {MG}  = \dfrac{1}{6}\overrightarrow b  - \dfrac{1}{6}\left( { - 2\overrightarrow c  + \overrightarrow b } \right) - \dfrac{1}{6}\left( { - 2\overrightarrow d  + \overrightarrow b } \right)\\ \Leftrightarrow \overrightarrow {MG}  = \dfrac{1}{6}\overrightarrow b  + \dfrac{1}{3}\overrightarrow c  - \dfrac{1}{6}\overrightarrow b  + \dfrac{1}{3}\overrightarrow d  - \dfrac{1}{6}\overrightarrow b \\ \Leftrightarrow \overrightarrow {MG}  =  - \dfrac{1}{6}\overrightarrow b  + \dfrac{1}{3}\overrightarrow c  + \dfrac{1}{3}\overrightarrow d \\ \Leftrightarrow \overrightarrow {MG}  =  - \dfrac{1}{6}\left( {\overrightarrow b  - 2\overrightarrow c  - 2\overrightarrow d } \right)\end{array}\)

Vậy \(\overrightarrow {MG}  =  - \dfrac{1}{6}\left( {\overrightarrow b  - 2\overrightarrow c  - 2\overrightarrow d } \right)\).

Chọn A.

Phương pháp giải:

Biến đổi vecto để đưa về \(MK = x\) với \(x\) là hằng số thì quỹ tích điểm \(M\) là mặt cầu tâm \(K\) có bán kính bằng \(x\).

Lời giải chi tiết:

Gọi \(G\) là trọng tâm tam giác \(ABC\).

Tam giác \(ABC\) là tam giác đều có cạn bằng 8 nên \(\left\{ \begin{array}{l}\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \\GA = GB = GC = \dfrac{{\sqrt 3 }}{3}AB = \dfrac{{8\sqrt 3 }}{3}\end{array} \right.\)

Ta có:

\(\begin{array}{l}M{A^2} + M{B^2} + M{C^2} = 100\\ \Leftrightarrow {\overrightarrow {MA} ^2} + {\overrightarrow {MB} ^2} + {\overrightarrow {MC} ^2} = 100\\ \Leftrightarrow {\left( {\overrightarrow {MG}  + \overrightarrow {GA} } \right)^2} + {\left( {\overrightarrow {MG}  + \overrightarrow {GB} } \right)^2} + {\left( {\overrightarrow {MG}  + \overrightarrow {GC} } \right)^2} = 100\\ \Leftrightarrow M{G^2} + 2\overrightarrow {MG} .\overrightarrow {GA}  + G{A^2} + M{G^2} + 2\overrightarrow {MG} .\overrightarrow {GB}  + G{B^2} + M{G^2} + 2\overrightarrow {MG} .\overrightarrow {GC}  + G{C^2} = 100\end{array}\)

\(\begin{array}{l} \Leftrightarrow 3M{G^2} + 2\overrightarrow {MG} \left( {\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC} } \right) + \left( {G{A^2} + G{B^2} + G{C^2}} \right) = 100\\ \Leftrightarrow 3M{G^2} + 2.\overrightarrow {MG} .\overrightarrow 0  + 3G{A^2} = 100\\ \Leftrightarrow 3M{G^2} + 3.{\left( {\dfrac{{8\sqrt 3 }}{3}} \right)^2} = 100\\ \Leftrightarrow M{G^2} = 12 \Leftrightarrow MG = 2\sqrt 3 \end{array}\)

Vậy quỹ tích điểm \(M\) là mặt cầu tâm \(G\) có bán kính bằng \(2\sqrt 3 \).

Chọn C.

Phương pháp giải:

- Hình hộp có tất cả các mặt đều là hình bình hành.

- Sử dụng công thức ba điểm: \(\overrightarrow {AC}  = \overrightarrow {AB}  + \overrightarrow {BC} \).

- Áp dụng công thức hình hành hành: Cho hình bình hành \(ABCD\), ta có: \(\overrightarrow {AC}  = \overrightarrow {AB}  + \overrightarrow {AD} \).

Lời giải chi tiết:

Ta có: \(\overrightarrow {AC'}  = \overrightarrow {AC}  + \overrightarrow {CC'} \).

Vì \(ABCD\) là hình bình hành nên \(\overrightarrow {AC}  = \overrightarrow {AB}  + \overrightarrow {AD} .\)

Lại có: \(\overrightarrow {CC'}  = \overrightarrow {AA'} \).

Do đó \(\overrightarrow {AC'}  = \overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'} .\)

Chọn C.

Phương pháp giải:

Áp dụng công thức tích vô hướng của 2 véctơ: Tích vô hướng của hai vectơ bằng tích độ dài nhân cos góc xen giữa.

Lời giải chi tiết:

\(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right).\)

Chọn B.

Phương pháp giải:

Điều kiện 3 véctơ đồng phẳng:

- Cùng song song với một mặt phẳng.

- Tồn tại \(m,\,\,n\,\,\left( {{m^2} + {n^2} > 0} \right)\) sao cho \(\overrightarrow c  = m\overrightarrow a  + n\overrightarrow b \).

Lời giải chi tiết:

Ta có \(ABCD\) là hình bình hành nên \(\overrightarrow {BD}  = \overrightarrow {BA}  + \overrightarrow {BC} \)

Mà \(\overrightarrow {BD}  = \overrightarrow {B'D'} \)\( \Rightarrow \overrightarrow {B'D'}  = \overrightarrow {BA}  + \overrightarrow {BC} \) .

Vậy \(\overrightarrow {B'D'} ;\,\,\overrightarrow {BA} ;\,\,\overrightarrow {BC} \) đồng phẳng.

Chọn B.

Phương pháp giải:

- Dựng vectơ gốc \(A\) bằng vectơ \(\overrightarrow {BC} \).

- Chứng minh \(\Delta ABC\) đều, sử dụng tính chất của tam giác đều.

Lời giải chi tiết:

Dựng hình bình hành \(ABCE\), khi đó ta có \(\overrightarrow {BC}  = \overrightarrow {AE} \).

\( \Rightarrow \angle \left( {\overrightarrow {AB} ;\overrightarrow {BC} } \right) = \angle \left( {\overrightarrow {AB} ;\overrightarrow {AE} } \right) = \angle BAE\).

Vì tứ diện \(ABCD\) đều nên \(AB = BC = CA \Rightarrow \Delta ABC\) đều.

Do đó \(\angle ABC = {60^0}\).

Mà \(ABCE\) là hình bình hành (theo cách dựng) nên \(\angle BAE = {180^0} - \angle ABC = {120^0}\).

Vậy \(\angle \left( {\overrightarrow {AB} ;\overrightarrow {BC} } \right) = {120^0}\).

Chọn C.

Phương pháp giải:

Áp dụng tính chất của trọng tâm tam giác.

Lời giải chi tiết:

Ta có \(G\) là trọng tâm tam giác \(BCD\) \( \Rightarrow \overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = 3\overrightarrow {AG} \)

Chọn B.

Phương pháp giải:

- Tính tích vô hướng \(\overrightarrow {SB} .\overrightarrow {AC} \).

- Sử dụng định nghĩa tích vô hướng \(\overrightarrow {SB} .\overrightarrow {AC}  = SB.AC.\cos \left( {\overrightarrow {SB} ;\overrightarrow {AC} } \right)\).

Lời giải chi tiết:

Ta có

\(\begin{array}{l}\overrightarrow {SB} .\overrightarrow {AC}  = \left( {\overrightarrow {SC}  + \overrightarrow {CB} } \right).\overrightarrow {AC} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \overrightarrow {SC} .\overrightarrow {AC}  + \overrightarrow {CB} .\overrightarrow {AC} \end{array}\)

+) \(\overrightarrow {SC} .\overrightarrow {AC}  = SC.AC.cos\angle \left( {\overrightarrow {SC} ;\overrightarrow {AC} } \right)\).

Xét \(\Delta SAC\) ta có \(SA = AC = SC = a \Rightarrow \Delta SAC\) đều \( \Rightarrow \angle \left( {\overrightarrow {SC} ;\overrightarrow {AC} } \right) = {60^0}\).

\( \Rightarrow \overrightarrow {SC} .\overrightarrow {AC}  = a.a.\cos {60^0} = \frac{1}{2}{a^2}\).

+) \(\overrightarrow {CB} .\overrightarrow {AC}  = CB.AC.\cos \angle \left( {\overrightarrow {CB} ;\overrightarrow {AC} } \right)\).

Xét tam giác \(ABC\) có \(AB = AC = a,\,\,BC = a\sqrt 2 \) \( \Rightarrow \Delta ABC\) vuông cân tại \(A\).

\( \Rightarrow \angle \left( {\overrightarrow {CB} ;\overrightarrow {AC} } \right) = {180^0} - {45^0} = {135^0}\).

\( \Rightarrow \overrightarrow {CB} .\overrightarrow {AC}  = a\sqrt 2 .a.\cos {135^0} =  - {a^2}\).

\(\begin{array}{l} \Rightarrow \overrightarrow {SB} .\overrightarrow {AC}  = \frac{1}{2}{a^2} - {a^2} =  - \frac{1}{2}{a^2}\\ \Rightarrow SB.AC.\cos \angle \left( {\overrightarrow {SB} ;\overrightarrow {AC} } \right) =  - \frac{1}{2}{a^2}\\ \Leftrightarrow a.a.\cos \angle \left( {\overrightarrow {SB} ;\overrightarrow {AC} } \right) =  - \frac{1}{2}{a^2}\\ \Leftrightarrow \cos \angle \left( {\overrightarrow {SB} ;\overrightarrow {AC} } \right) =  - \frac{1}{2}\\ \Leftrightarrow \angle \left( {\overrightarrow {SB} ;\overrightarrow {AC} } \right) = {120^0}\end{array}\).

Chọn D.

Phương pháp giải:

Sử dụng công thức trọng tâm: \(\overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \) với \(G\) là trọng tâm của \(\Delta BCD\).

Lời giải chi tiết:

Vì \(G\) là trọng tâm tam giác \(BCD\) nên ta có: \(\overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \).

\(\begin{array}{l} \Leftrightarrow \overrightarrow {GA}  + \overrightarrow {AB}  + \overrightarrow {GA}  + \overrightarrow {AC}  + \overrightarrow {GA}  + \overrightarrow {AD}  = \overrightarrow 0 \\ \Leftrightarrow 3\overrightarrow {GA}  + \left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right) = \overrightarrow 0 \\ \Leftrightarrow 3\overrightarrow {AG}  = \overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} \\ \Leftrightarrow \overrightarrow {AG}  = \dfrac{1}{3}\left( {\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD} } \right)\end{array}\)

Vậy khẳng định đúng là A.

Chọn A.

Phương pháp giải:

Sử dụng công thức trung điểm: \(\overrightarrow {AM}  = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AB'} } \right)\) và công thức hình bình hành: \(\overrightarrow {AB'}  = \overrightarrow {AB}  + \overrightarrow {AA'} \).

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}\overrightarrow {AM}  = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AB'} } \right)\\\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AB}  + \overrightarrow {AA'} } \right)\\\,\,\,\,\,\,\,\,\,\, = \overrightarrow {AB}  + \dfrac{1}{2}\overrightarrow {AA'} \\\,\,\,\,\,\,\,\,\, = \overrightarrow {CB}  - \overrightarrow {CA}  + \dfrac{1}{2}\overrightarrow {AA'} \\\,\,\,\,\,\,\,\,\, = \overrightarrow b  - \overrightarrow a  + \dfrac{1}{2}\overrightarrow c \end{array}\)

Chọn D.

Phương pháp giải:

Sử dụng công thức trọng tâm: G là trọng tâm của tam giác BCD thì \(\overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \).

Lời giải chi tiết:

Vì G là trọng tâm của tam giác BCD thì \(\overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \).

Chọn D.

Phương pháp giải:

Sử dụng công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\overrightarrow {\left| b \right|} .\cos \angle \left( {\overrightarrow a ;\overrightarrow b } \right)\).

Lời giải chi tiết:

Vì \(\overrightarrow {AC} ;\,\,\overrightarrow {A'C'} \) là 2 vectơ cùng phương \( \Rightarrow \angle \left( {\overrightarrow {AB} ;\overrightarrow {A'C'} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = \angle BAC = {45^0}\).

Do A’B’C’D’ là hình vuông cạnh a nên \(A'C' = a\sqrt 2 \).

Vậy \(\overrightarrow {AB} .\overrightarrow {A'C'}  = AB.A'C'.\cos {45^0} = a.a\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = {a^2}\).

Chọn B.

Phương pháp giải:

- Gọi \(I = AB' \cap A'B\) và E là trung điểm của CD’, xác định tọa độ điểm I và E.

- Giải phương trình \(\overrightarrow {BI}  = \overrightarrow {CE} \).

Lời giải chi tiết:

Gọi \(I = AB' \cap A'B\), vì ABB’A’ là hình bình hành nên I là trung điểm của A’B và AB’ \( \Rightarrow I\left( {\frac{3}{2};1;1} \right)\).

Gọi E là trung điểm của CD’ \( \Rightarrow E\left( {\frac{1}{2};2; - 3} \right)\).

Xét tứ giác A’D’CB có A’D’ // BC, A’D’ = BC \( \Rightarrow A'D'CB\) là hình bình hành \( \Rightarrow A'B\parallel CD'\) và A’B = CD’.

\( \Rightarrow BI\parallel CE\) và BI = CE, do đó \(\overrightarrow {BI}  = \overrightarrow {CE} \).

Ta có \(\overrightarrow {CE}  = \left( { - \frac{5}{2};2;0} \right)\).

\( \Rightarrow \left\{ \begin{array}{l}\frac{3}{2} - {x_B} =  - \frac{5}{2}\\1 - {y_B} = 2\\1 - {z_B} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = 4\\{y_B} =  - 1\\{z_B} = 1\end{array} \right. \Rightarrow B\left( {4; - 1;1} \right)\).

Chọn A.

Phương pháp giải:

Áp dụng công thức tính tọa độ vectơ trong không gian.

Lời giải chi tiết:

Ta có \(A\left( {2;3; - 1} \right),B\left( { - 4;1;9} \right) \Rightarrow \overrightarrow {AB}  = \left( { - 6; - 2;10} \right)\).

Chọn B.

Phương pháp giải:

Sử dụng công thức \(\cos \left( \overrightarrow{a};\overrightarrow{b} \right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left| \overrightarrow{a} \right|.\left| \overrightarrow{b} \right|}\).

Lời giải chi tiết:

Ta có: \(\cos \left( \overrightarrow{MN},\overrightarrow{AC'} \right)=\frac{\overrightarrow{MN}.\overrightarrow{AC'}}{\left| \overrightarrow{MN} \right|.\left| \overrightarrow{AC'} \right|}\)

Gọi cạnh của hình lập phương bằng a.

\(AM\bot \left( ABB'A' \right)\Rightarrow AM\bot AN\Rightarrow \Delta AMN\) vuông tại A

\(\begin{align}  & M{{N}^{2}}=M{{A}^{2}}+A{{N}^{2}}=M{{A}^{2}}+A{{B}^{2}}+B{{N}^{2}} \\  & =\frac{{{a}^{2}}}{4}+{{a}^{2}}+\frac{{{a}^{2}}}{4}=\frac{3{{a}^{2}}}{2}\Rightarrow MN=\frac{a\sqrt{3}}{\sqrt{2}} \\ \end{align}\)

\(B'C'\bot \left( ABB'A' \right)\Rightarrow B'C'\bot AB'\Rightarrow \Delta B'C'\) vuông tại B’.

\(\begin{align}  & C'{{A}^{2}}=C'B{{'}^{2}}+B'{{A}^{2}}=C'B{{'}^{2}}+B'{{B}^{2}}+B{{A}^{2}} \\  & ={{a}^{2}}+{{a}^{2}}+{{a}^{2}}=3{{a}^{2}}\Rightarrow C'A=a\sqrt{3} \\ \end{align}\)

Lại có:

\(\begin{align}  & \overrightarrow{MN}.\overrightarrow{AC'}=\left( \overrightarrow{MA}+\overrightarrow{AB}+\overrightarrow{BN} \right)\left( \overrightarrow{AB}+\overrightarrow{BB'}+\overrightarrow{B'C'} \right) \\  & =\overrightarrow{MA}.\overrightarrow{AB}+A{{B}^{2}}+\overrightarrow{BN}.\overrightarrow{AB}+\overrightarrow{MA}.\overrightarrow{BB'}+\overrightarrow{AB}.\overrightarrow{BB'}+\overrightarrow{BN}.\overrightarrow{BB'}+\overrightarrow{MA}.\overrightarrow{B'C'}+\overrightarrow{AB}.\overrightarrow{B'C'}+\overrightarrow{BN}.\overrightarrow{B'C'} \\ \end{align}\)

Mà \(\overrightarrow{MA}.\overrightarrow{AB}=\overrightarrow{BN}.\overrightarrow{AB}=\overrightarrow{MA}.\overrightarrow{BB'}=\overrightarrow{AB}.\overrightarrow{BB'}=\overrightarrow{AB}.\overrightarrow{B'C'}=\overrightarrow{BN}.\overrightarrow{B'C'}=0\) (do các tích vô hướng của các vector vuông góc)

Nên \(\overrightarrow{MN}.\overrightarrow{AC'}=A{{B}^{2}}+\overrightarrow{BN}.\overrightarrow{BB'}+\overrightarrow{MA}.\overrightarrow{B'C'}={{a}^{2}}+\frac{{{a}^{2}}}{2}-\frac{{{a}^{2}}}{2}={{a}^{2}}\)

Vậy \(\cos \left( \overrightarrow{MN},\overrightarrow{AC'} \right)=\frac{\overrightarrow{MN}.\overrightarrow{AC'}}{\left| \overrightarrow{MN} \right|.\left| \overrightarrow{AC'} \right|}=\frac{{{a}^{2}}}{\frac{a\sqrt{3}}{\sqrt{2}}.a\sqrt{3}}=\frac{\sqrt{2}}{3}\)

Chọn B.

Phương pháp giải:

Sử dụng các tính chất của hình lập phương và quy tắc trung điểm để cộng các véc tơ.

Nếu \(I\) là trung điểm của \(AB\)thì \(\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}\).

Lời giải chi tiết:

Gọi \({O}'\) là tâm của hình vuông \({A}'{B}'{C}'{D}'\).

Ta có :

\(\overrightarrow{OS}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{O{A}'}+\overrightarrow{O{B}'}+\overrightarrow{O{C}'}+\overrightarrow{O{D}'}\)

\(=\left( \overrightarrow{OA}+\overrightarrow{OC} \right)+\left( \overrightarrow{OB}+\overrightarrow{OD} \right)+\left( \overrightarrow{O{A}'}+\overrightarrow{O{C}'} \right)+\left( \overrightarrow{O{B}'}+\overrightarrow{O{D}'} \right)\).

\(=\overrightarrow{0}+2\overrightarrow{O{O}'}+2\overrightarrow{O{O}'}=4\overrightarrow{O{O}'}\).

Do đó \(OS=\left| 4\overrightarrow{O{O}'} \right|=4.\left| \overrightarrow{O{O}'} \right|=4a\).

Chọn B.

Phương pháp giải:

Sử dụng công thức \(\overrightarrow a .\overrightarrow b  = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ;\overrightarrow b } \right)\) và định lí Cosin trong tam giác.

Lời giải chi tiết:

\(\begin{array}{l}\cos \left( {\overrightarrow {AB} ;\overrightarrow {CD} } \right) = \frac{{\overrightarrow {AB} .\overrightarrow {CD} }}{{AB.CD}} = \frac{{\overrightarrow {AB} \left( {\overrightarrow {AD}  - \overrightarrow {AC} } \right)}}{{AB.CD}} = \frac{{\overrightarrow {AB} .\overrightarrow {AD}  - \overrightarrow {AB} .\overrightarrow {AC} }}{{AB.CD}}\\ = \frac{{AB.AD.\cos \left( {AB;AD} \right) - AB.AC.\cos \left( {AB;AC} \right)}}{{AB.CD}}\\ = \frac{{A{B^2} + A{D^2} - B{D^2} - \left( {A{B^2} + A{C^2} - B{C^2}} \right)}}{{2AB.CD}}\\ =  - \frac{1}{2} \Rightarrow \left( {\overrightarrow {AB} ;\overrightarrow {CD} } \right) = {120^0} \Rightarrow \left( {AB;CD} \right) = {60^0}\end{array}\)

Chọn A.