Phương pháp giải:

*) Gọi phương trình đường thẳng OA có dạng \(ax + by = 0\,\,\left( {{a^2} + {b^2} \ne 0} \right)\), tìm tọa độ điểm A là giao điểm của OA và elip. Tương tự như vậy tìm tọa độ điểm B.

*) Tính độ dài \(OA,OB\) và say ra tổng \({1 \over {O{A^2}}} + {1 \over {O{B^2}}}\) không đổi.

*) Sử dụng BĐT Cô si:  \({1 \over {O{A^2}}} + {1 \over {O{B^2}}} \ge {2 \over {OA.OB}} = {1 \over {{S_{OAB}}}} \Rightarrow {S_{OAB}} \ge {1 \over {{1 \over {O{A^2}}} + {1 \over {O{B^2}}}}}\). Dấu bằng xảy ra \( \Leftrightarrow OA = OB\)

*) Suy ra tính chất đặc biệt của tam giác OAB, của điểm A và điểm B sau đó tìm tọa độ của chúng.

Lời giải chi tiết:

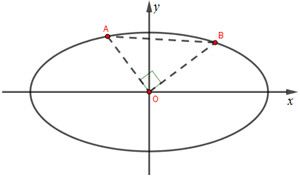
Gọi đường thẳng OA có phương trình \(ax + by = 0\,\,\left( {{a^2} + {b^2} \ne 0} \right)\), khi đó tọa độ của điểm \(A\left( {{x_0};{y_0}} \right)\) là nghiệm của hệ phương trình: \(\left\{ \matrix{  a{x_0} + b{y_0} = 0 \hfill \cr   {{x_0^2} \over 4} + y_0^2 = 1 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  {y_0} =  - {a \over b}{x_0} \hfill \cr   {{x_0^2} \over 4} = 1 - y_0^2 \hfill \cr}  \right.\)

\(\eqalign{  &  \Leftrightarrow {{x_0^2} \over 4} = 1 - {{{a^2}} \over {{b^2}}}x_0^2 \Leftrightarrow \left( {{1 \over 4} + {{{a^2}} \over {{b^2}}}} \right)x_0^2 = 1 \Leftrightarrow {{4{a^2} + {b^2}} \over {4{b^2}}}x_0^2 = 1 \Leftrightarrow x_0^2 = {{4{b^2}} \over {4{a^2} + {b^2}}} \Rightarrow y_0^2 = {{4{a^2}} \over {4{a^2} + {b^2}}}  \cr   &  \Rightarrow O{A^2} = x_0^2 + y_0^2 = {{4{b^2}} \over {4{a^2} + {b^2}}} + {{4{a^2}} \over {4{a^2} + {b^2}}} = {{4\left( {{a^2} + {b^2}} \right)} \over {4{a^2} + {b^2}}} \cr} \)

Tương tự như vậy ta tính được \(O{B^2} = {{4\left( {{a^2} + {b^2}} \right)} \over {{a^2} + 4{b^2}}}\)

\( \Rightarrow {1 \over {O{A^2}}} + {1 \over {O{B^2}}} = {{{a^2} + 4{b^2}} \over {4\left( {{a^2} + {b^2}} \right)}} + {{4{a^2} + {b^2}} \over {4\left( {{a^2} + {b^2}} \right)}} = {{5{a^2} + 5{b^2}} \over {4\left( {{a^2} + {b^2}} \right)}} = {5 \over 4}\)

Ta có:

\(\eqalign{  & {1 \over {{a^2}}} + {1 \over {{b^2}}} = {1 \over {O{A^2}}} + {1 \over {O{B^2}}} \ge {2 \over {OA.OB}} = {1 \over {{S_{OAB}}}}  \cr   &  \Leftrightarrow {5 \over 4} \ge {1 \over {{S_{OAB}}}} \Leftrightarrow {S_{OAB}} \le {4 \over 5} \cr} \)

\({S_{OAB\,\,Min}} = {4 \over 5} \Leftrightarrow OA = OB \Rightarrow \) Tam giác OAB vuông cân tại O.

Mà A, B trên (E), có tung độ dương \( \Rightarrow \) A, B đối xứng nhau qua Oy, đồng thời A, B nằm trên các tia phân giác của các góc phần tư.

Giả sử, \(A \in d:\,\,y = x \Rightarrow A\left( {{x_0};{x_0}} \right),\,\,{x_0} > 0\)

\(A \in (E) \Rightarrow {{{x_0}^2} \over 4} + {{{x_0}^2} \over 1} = 1 \Leftrightarrow {x_0}^2 = {4 \over 5} \Leftrightarrow \left[ \matrix{  {x_0} = {2 \over {\sqrt 5 }}\,\,(TM) \hfill \cr   {x_0} =  - {2 \over {\sqrt 5 }}\,\,(L) \hfill \cr}  \right. \Rightarrow A\left( {{2 \over {\sqrt 5 }};{2 \over {\sqrt 5 }}} \right),\,B\left( { - {2 \over {\sqrt 5 }};{2 \over {\sqrt 5 }}} \right)\,\)     

Nếu \(A \in d':\,\,y =  - x\), tương tự ta tìm được : \(A\left( { - {2 \over {\sqrt 5 }};{2 \over {\sqrt 5 }}} \right),\,B\left( {{2 \over {\sqrt 5 }};{2 \over {\sqrt 5 }}} \right)\,\)

Chọn: B.