Phương pháp giải:

Lấy \(A\left( {{x_0};{y_0}} \right) \in \left( E \right)\), xác định điểm B đối xứng với A qua Ox.

Tam giác ABC đều \( \Leftrightarrow AB = AC\), giải phương trình tìm \({x_0};{y_0}\).

Lời giải chi tiết:

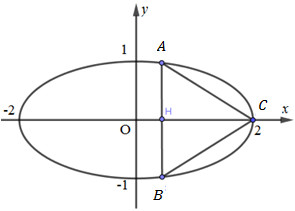
Giả sử \(A\left( {{x_0};{y_0}} \right)\). Do A, B đối xứng nhau qua Ox nên \(B({x_0}; - {y_0})\).

Ta có: \(A{B^2} = 4{y_0}^2,\,\,\,A{C^2} = {({x_0} - 2)^2} + {y_0}^2\)

Vì \(A \in \left( E \right) \Rightarrow {{{x_0}^2} \over 4} + {y_0}^2 = 1 \Rightarrow {y_0}^2 = 1 - {{{x_0}^2} \over 4}\,\,\,\,\left( 1 \right)\)

Vì \(AB = AC \Rightarrow {({x_0} - 2)^2} + {y_0}^2 = 4{y_0}^2\,\,\,\,\,\left( 2 \right)\)

Thay (1) vào (2) và rút gọn ta được :

\(7{x_0}^2 - 16{x_0} + 4 = 0 \Leftrightarrow \left[ \matrix{  {x_0} = 2 \hfill \cr   {x_0} = {2 \over 7} \hfill \cr}  \right.\)

Với \({x_0} = 2 \Rightarrow {y_0} = 0\,\,(L)\) vì trùng với điểm C.

Với \({x_0} = {2 \over 7} \Rightarrow {y_0} =  \pm {{4\sqrt 3 } \over 7}\).

Vậy, \(A\left( {{2 \over 7};{{4\sqrt 3 } \over 7}} \right),\,\,B\left( {{2 \over 7}; - {{4\sqrt 3 } \over 7}} \right)\) hoặc \(A\left( {{2 \over 7}; - {{4\sqrt 3 } \over 7}} \right),\,\,B\left( {{2 \over 7};{{4\sqrt 3 } \over 7}} \right)\). 

Chọn: C.