Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho hình lập phương \(ABCD.{A}'{B}'{C}'{D}'\) có cạnh bằng \(a\) Gọi \(O\) là tâm của hình vuông \(ABCD\) và điểm \(S\) sao cho \(\overrightarrow{OS}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{O{A}'}+\overrightarrow{O{B}'}+\overrightarrow{O{C}'}+\overrightarrow{O{D}'}\). Tính độ dài đoạn \(OS\) theo \(a\).
- A \(OS=6a\).
- B \(OS=4a\).
- C \(OS=a\).
- D \(OS=2a\).
Phương pháp giải:
Sử dụng các tính chất của hình lập phương và quy tắc trung điểm để cộng các véc tơ.
Nếu \(I\) là trung điểm của \(AB\)thì \(\overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}\).
Lời giải chi tiết:
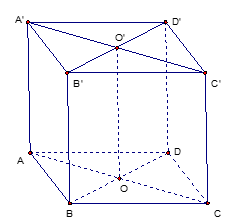
Gọi \({O}'\) là tâm của hình vuông \({A}'{B}'{C}'{D}'\).
Ta có :
\(\overrightarrow{OS}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{O{A}'}+\overrightarrow{O{B}'}+\overrightarrow{O{C}'}+\overrightarrow{O{D}'}\)
\(=\left( \overrightarrow{OA}+\overrightarrow{OC} \right)+\left( \overrightarrow{OB}+\overrightarrow{OD} \right)+\left( \overrightarrow{O{A}'}+\overrightarrow{O{C}'} \right)+\left( \overrightarrow{O{B}'}+\overrightarrow{O{D}'} \right)\).
\(=\overrightarrow{0}+2\overrightarrow{O{O}'}+2\overrightarrow{O{O}'}=4\overrightarrow{O{O}'}\).
Do đó \(OS=\left| 4\overrightarrow{O{O}'} \right|=4.\left| \overrightarrow{O{O}'} \right|=4a\).
Chọn B.













