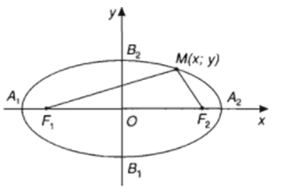
Câu hỏi 3 trang 86 SGK Hình học 10

Đề bài

Trong phương trình (1) hãy giải thích vì sao ta luôn đặt được \(b^2=a^2-c^2\).

Lời giải chi tiết

Do \(F_1(-c;0),F_2(c;0)\) nên \(OF_1=OF_2=c\)

\(B_1(0;-b),B_2(0;b)\)

\( \Rightarrow {B_2}{F_1} = {B_2}{F_2} = \sqrt {{b^2} + {c^2}} \)

Do \(B_2\) thuộc elip nên:

\(\eqalign{
& {B_2}{F_1} + {B_2}{F_2} = 2a \Rightarrow 2\sqrt {{b^2} + {c^2}} = 2a \cr
& \Rightarrow {b^2} + {c^2} = {a^2} \Leftrightarrow {b^2} = {a^2} - {c^2} \cr} \)

Cách khác:

Do \(F_1(-c;0),F_2(c;0)\) nên \({F_1}{F_2} = 2c\).

Xét tam giác \(MF_1F_2\) có:

\(M{F_1} + M{F_2} > {F_1}{F_2}\) \( \Rightarrow 2a > 2c \) \(\Leftrightarrow a > c \) \(\Rightarrow {a^2} - {c^2} > 0\)

Do đó có thể đặt \({b^2} = {a^2} - {c^2}\).

HocTot.Nam.Name.Vn