Nội dung từ Loigiaihay.Com
Câu hỏi:
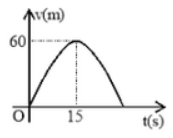
Một xe ô tô sau khi chờ hết đèn đỏ thì bắt đầu phóng nhanh với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường cong parabol có hình bên. Biết rằng sau 15 giây thì xe đạt đến vận tốc cao nhất \(60m/s\) và bắt đầu giảm tốc độ. Hỏi từ lúc bắt đầu đến lúc đạt vận tốc cao nhất thì xe đi được quãng đường bao nhiêu mét?
- A \(700m\)
- B \(1200m\)
- C \(500m\)
- D \(600m\)
Phương pháp giải:
Tìm hàm số v(t) dựa vào đồ thị.
\(s\left( t \right) = \int\limits_0^t {v\left( t \right)dt} \) là quãng đường xe đi được đến thời điểm t.
Lời giải chi tiết:
Từ đồ thị ta thấy, \(v\left( t \right) = a{t^2} + bt + c\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l} - \dfrac{b}{{2a}} = 15\\a{.15^2} + b.15 + c = 60\\c = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{4}{{15}}\\b = 8\\c = 0\end{array} \right. \Rightarrow v\left( t \right) = - \dfrac{4}{{15}}{t^2} + 8t\end{array}\)
\(s\left( t \right) = \int\limits_0^t {v\left( t \right)dt} \) là quãng đường xe đi được đến thời điểm t.
\( \Rightarrow s\left( {15} \right) = \int\limits_0^{15} {v\left( t \right)dt} = 600\)













