Câu hỏi trước
Nội dung từ Loigiaihay.Com
Câu hỏi:
Trong không gian, cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\). Vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) bằng
- A \(\overrightarrow {AC'} \)
- B \(\overrightarrow {AD'} \).
- C \(\overrightarrow {AB'} \)
- D \(\overrightarrow {AC} \).
Phương pháp giải:
Sử dụng quy tắc hình bình hành.
Lời giải chi tiết:
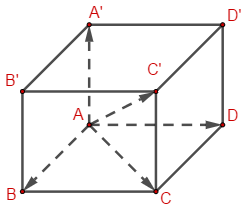
ABCD là hình bình hành nên \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
\(ACC'A'\) là hình bình hành \(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)