Phương pháp giải:

Áp dụng định luật bảo toàn động lượng.

Lời giải chi tiết:

Khi đạn nổ, lực tác dụng của không khí rất nhỏ so với nội lực nên được coi như là một hệ kín.

a)

Viên đạn đang bay thẳng đứng, nổ thành 2 mảnh, mảnh thứ nhất bay theo phương ngang nên suy ra \(\overrightarrow p  \bot \overrightarrow {{p_1}} \)

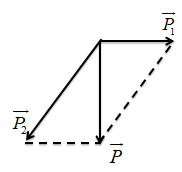
Áp dụng định luật bảo toàn động lượng ta có:

\(\overrightarrow p  = \overrightarrow {{p_1}}  + \overrightarrow {{p_2}} \)

\( \Leftrightarrow p_2^2 = {p^2} + p_1^2\)

\( \Leftrightarrow {p_2} = \sqrt {{{\left( {m.v} \right)}^2} + {{\left( {{m_1}.{v_1}} \right)}^2}} \)

\( \Leftrightarrow {p_2} = \sqrt {{{\left( {10.85} \right)}^2} + {{\left( {6.64} \right)}^2}}  = 932,7\left( {kg.m/s} \right)\)

Độ lớn vận tốc của mảnh thứ hai là:

\({v_2} = \frac{{{p_2}}}{{{m_2}}} = \frac{{{p_2}}}{{m - {m_1}}} = \frac{{932,7}}{{10 - 6}} = 233m/s\)

b)

Nếu mảnh thứ nhất chếch lên hợp với phương ngang góc 30⁰ suy ra \(\widehat {\left( {\overrightarrow p ,\overrightarrow {{p_1}} } \right)} = 90 + 30 = {120^0}\)

Khi đó, ta có:

\(p_2^2 = {p^2} + p_1^2 + 2p.{p_1}.\cos {120^0}\)

\( \Leftrightarrow {p_2} = \sqrt {{{\left( {m.v} \right)}^2} + {{\left( {{m_1}.{v_1}} \right)}^2} + 2mv.{m_1}{v_1}.\cos 120} \)

\( \Leftrightarrow {p_2} = \sqrt {{{\left( {10.85} \right)}^2} + {{\left( {6.64} \right)}^2} + 2.10.85.6.64.( - \frac{1}{2})}  = 932,7\left( {kg.m/s} \right)\)

\( \Leftrightarrow {p_2} = 737,3\left( {kg.m/s} \right)\)

Độ lớn vận tốc của mảnh thứ hai khi đó là:

\({v_2} = \frac{{{p_2}}}{{{m_2}}} = \frac{{737,3}}{{10 - 6}} = 184\left( {m/s} \right)\)

- Khi lên đến vị trí cao nhất thì vận tốc của vật bằng 0. Ta có:

\({v^2} - v_1^2 = 2gh\)

\( \Leftrightarrow h = \frac{{{0^2} - {{64}^2}}}{{2.( - 10)}} = 204,8m\)

Vậy độ cao nhất mà mảnh thứ nhất có thể lên đến so với điểm M là 204,8m.