Nội dung từ Loigiaihay.Com
Câu hỏi:
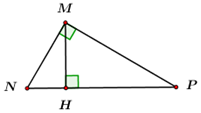
Cho \(\Delta MNP\) vuông tại \(M\), đường cao \(MH\). Khẳng định nào sau đây đúng?
- A \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{M{N^2}}}.\dfrac{1}{{M{P^2}}}.\)
- B \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{M{N^2}}} - \dfrac{1}{{M{P^2}}}.\)
- C \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}}.\)
- D \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{MN}} + \dfrac{1}{{MP}}.\)
Phương pháp giải:
Sử dụng hệ thức lượng trong tam giác vuông.
Lời giải chi tiết:
Xét tam giác \(MNP\) vuông tại \(M\), đường cao \(MH\) ta có: \(\dfrac{1}{{M{H^2}}} = \dfrac{1}{{M{N^2}}} + \dfrac{1}{{M{P^2}}}\).
Vậy khẳng định C đúng.
Chọn C.