Nội dung từ Loigiaihay.Com
Câu hỏi:
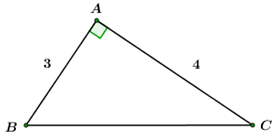
Cho tam giác \(ABC\) vuông tại \(A\), biết \(AB{\rm{ }} = {\rm{ 3}}cm,{\rm{ }}AC{\rm{ }} = 4cm.\) Giải tam giác \(ABC\).
- A \(BC = 5cm\,\,;\,\,\,\angle B = {60^0}\,\,\,;\,\,\,\angle C = {30^0}\)
- B \(BC = 5cm\,\,;\,\,\,\angle B = {48^0}35'\,\,\,;\,\,\,\angle C = {41^0}25'\)
- C \(BC = 5cm\,\,;\,\,\,\angle B = {41^0}25'\,\,\,;\,\,\,\angle C = {48^0}35'\)
- D \(BC = 5cm\,\,;\,\,\,\angle B = {53^0}8'\,\,\,;\,\,\,\angle C = {36^0}52'\)
Phương pháp giải:
Sử dụng định lý Pitago để tính cạnh BC.
Sử dụng định nghĩa tỉ số lượng giác, tính chất hai góc phụ nhau.
Từ tỉ số lượng giác suy ra số đo góc
Lời giải chi tiết:
Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có:
\(A{B^2} + A{C^2} = B{C^2} \Leftrightarrow B{C^2} = {3^2} + {4^2} = 25 \Rightarrow BC = 5\)
Xét \(\Delta ABC\) vuông tại \(A\) ta có:
\(sinB = \frac{{AC}}{{BC}} = \frac{4}{5} \Rightarrow \angle B \approx {53^0}8'\)
Vì \(\Delta ABC\) vuông tại \(A\) ta có:
\(\angle B + \angle C = {90^0} \Leftrightarrow {53^0}8' + \angle C = {90^0} \Leftrightarrow \angle C \approx {36^0}52'\)
Chọn D.