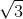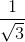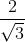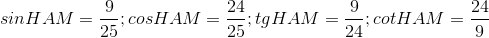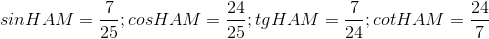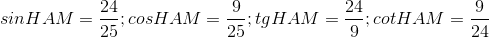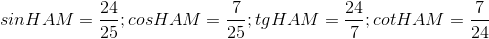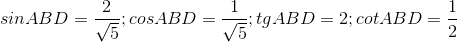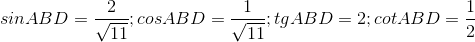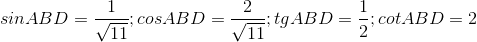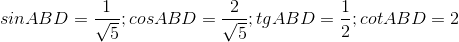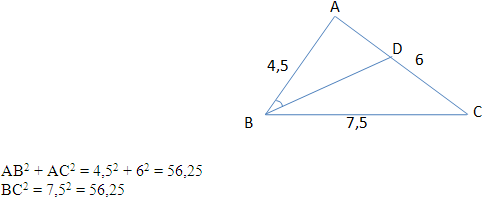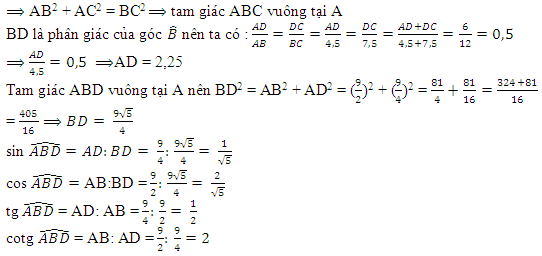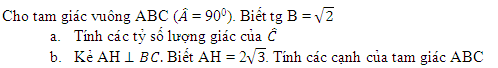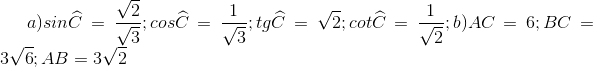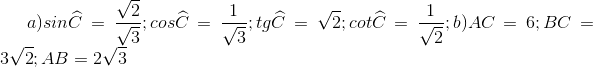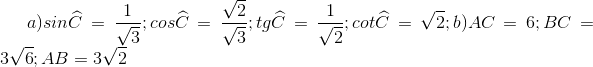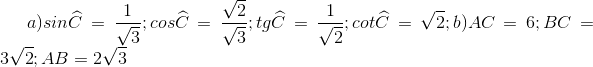40 bài tập tổng hợp về Tỉ số lượng giác của góc nhọnLàm bàiCâu hỏi 1 : Cho tam giác ABC vuông tại A. Trong các hệ thức sau, hệ thức đúng là:
Đáp án: C Phương pháp giải: Ghi nhớ các công thức lượng giác Lời giải chi tiết: Tam giác ABC vuông tại A nên ta có: \(\begin{array}{l} + )\sin C = \frac{{AB}}{{BC}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + )cosC = \frac{{AC}}{{BC}}\\ + )\tan C = \frac{{AB}}{{AC}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; + )\cot C = \frac{{AC}}{{AB}}\end{array}\) Chọn đáp án C. Câu hỏi 2 : Cho \(\Delta ABC\) vuông tại\(A.\) Khẳng định nào sau đây là đúng?
Đáp án: D Phương pháp giải: Sử dụng công thức tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết: Ta có: \(\sin B = \frac{{AC}}{{BC}}.\) Chọn D. Câu hỏi 3 : Cho \(\Delta ABC\) vuông tại \(A,\,\,\angle B = \alpha ,\,\,\angle C = \beta .\) Hệ thức nào sau đây luôn đúng?
Đáp án: B Phương pháp giải: Trong \(\Delta ABC\) vuông tại \(A\) ta có: \(\sin B = \cos C;\,\,\,\cos B = \sin C;\,\,\,\tan B = \cot C;\,\,\cot B = \tan C.\) Lời giải chi tiết: Trong các đáp án đã cho, chỉ có đáp án B luôn đúng. Chọn B. Câu hỏi 4 : Cho tam giác vuông \(ABC\) như hình vẽ bên. Khẳng định nào dưới đây đúng?
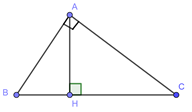
Đáp án: A Phương pháp giải: Trong tam giác vuông, cos của một góc bằng độ dài cạnh kề góc đó chia cho độ dài cạnh huyền. Lời giải chi tiết: Trong tam giác vuông \(ABH\) có \(\cos B = \frac{{BH}}{{AB}}.\) Chọn A. Câu hỏi 5 : Cho tam giác \(ABC\) vuông tại \(A,\) \(BC = a,\,\,AC = b,\,\,AB = c.\) Khẳng định nào dưới đây đúng?
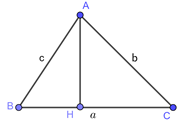
Đáp án: C Phương pháp giải: Sử dụng các công thức liên hệ giữa các cạnh và tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết: Xét \(\Delta ABC\) vuông tại\(A\) ta có: \(\sin B = \frac{{AC}}{{BC}} = \frac{b}{a} \Rightarrow b = a.\sin B\) Chọn C. Câu hỏi 6 : Cho tam giác \(ABC\) vuông tại \(A.\) Khẳng định nào dưới đây đúng?
Đáp án: B Phương pháp giải: Áp dụng các công thức tỉ số lượng giác của góc nhọn trong tam giác vuông: tan = cạnh đối/ cạnh kề. Lời giải chi tiết: Xét tam giác \(ABC\) vuông tại \(A\) ta có: \(\tan C = \frac{{AB}}{{AC}}.\) Chọn B. Câu hỏi 7 : Cho tam giác \(ABC\) vuông tại \(A.\) Khi đó trong các khẳng định sau, khẳng định nào đúng?
Đáp án: B Phương pháp giải: Sử dụng các công thức lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết: Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(\left\{ \begin{array}{l}\sin B = \cos C = \frac{{AC}}{{BC}}\\\cos B = \sin C = \frac{{AB}}{{BC}}\\\tan B = \cot C = \frac{{AC}}{{AB}}\\\cot B = \tan C = \frac{{AB}}{{AC}}\end{array} \right.\) Chọn B. Câu hỏi 8 : Cho hình vẽ. Tính tỉ số lượng giác của \(\angle B\) từ đó suy ra tỉ số lượng giác của \(\angle C\)
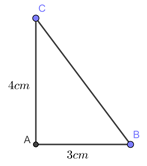
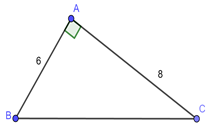
Đáp án: A Phương pháp giải: Sử dụng định lý Pi-ta-go. Sử dụng định nghĩa tỉ số lượng giác, tính chất hai góc phụ nhau. Lời giải chi tiết: Xét \(\Delta ABC\) vuông tại \(A\) có : \(A{B^2} + A{C^2} = B{C^2}\) (Định lý Pi-ta-go) \( \Leftrightarrow B{C^2} = {6^2} + {8^2} = 100 \Rightarrow BC = 10\,\,cm.\) Trong \(\Delta ABC\) vuông tại \(A\) ta có: \(\sin B = \frac{{AC}}{{BC}} = \frac{8}{{10}} = \frac{4}{5}\) \(\cos B = \frac{{AB}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\) \(\tan B = \frac{{AC}}{{AB}} = \frac{8}{6} = \frac{4}{3}\) \(\cot B = \frac{{AB}}{{AC}} = \frac{6}{8} = \frac{3}{4}\) Vì \(\angle B + \angle C = {90^0}\) \( \Rightarrow \sin C = \cos B = \frac{3}{5}\) \(\cos C = \sin B = \frac{4}{5}\) \(\tan C = \cot B = \frac{3}{4}\) \(\cot C = \tan B = \frac{4}{3}\) Chọn A. Câu hỏi 9 : Dựng góc \(\alpha \) biết: a) \(\tan \alpha = \frac{3}{4}\) b) \(\sin \alpha = \frac{3}{5}\) Phương pháp giải: Sử dụng định nghĩa tỉ số lượng giác. Lời giải chi tiết: a) \(\tan \alpha = \frac{3}{4}\) Dựng \(\angle xOy = {90^0}\) Lấy điểm \(A \in Ox\) sao cho \(OA = 3\) Lấy điểm \(B \in Oy\) sao cho \(OB = 4\) Khi đó ta được \(\alpha = \angle OBA\) vì \(\tan \angle OBA = \frac{3}{4}\) b) \(\sin \alpha = \frac{3}{5}\) Dựng \(\angle xOy = {90^0}\) Lấy điểm \(A \in Ox\) sao cho \(OA = 3\) Dựng đường tròn \(\left( {A;5} \right) \cap Oy = \left\{ B \right\}\) \( \Rightarrow \alpha = \angle ABO\) Khi đó ta được \(\alpha = \angle OBA\) vì \(\sin \angle ABO = \frac{3}{5}\) Câu hỏi 10 : Cho tam giác \(ABC\) vuông tại \(A\). Biết \(AB{\rm{ }} = {\rm{ 7}}cm,{\rm{ }}AC{\rm{ }} = 21cm.\) Tính các tỉ số lượng giác của góc \(B\) và \(C.\)
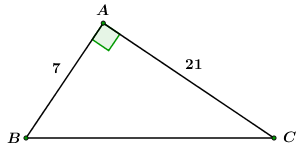
Đáp án: A Phương pháp giải: Sử dụng định lý Pi-ta-go để tính cạnh BC. Cho \(\angle B + \angle C = {90^0}.\) Khi đó ta có: \(\left\{ \begin{array}{l}\sin B = \cos C\\\cos B = \sin C\\\tan B = \cot C\\\cot B = \tan C.\end{array} \right.\) Lời giải chi tiết: Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có : \(A{B^2} + A{C^2} = B{C^2}\) \( \Leftrightarrow B{C^2} = {7^2} + {21^2} = 490\)\( \Rightarrow BC = 7\sqrt {10} \,\,\,cm.\) Trong \(\Delta ABC\) vuông tại \(A\) ta có: \(\sin B = \frac{{AC}}{{BC}} = \frac{{21}}{{7\sqrt {10} }} = \frac{3}{{\sqrt {10} }}\) \(\cos B = \frac{{AB}}{{BC}} = \frac{7}{{7\sqrt {10} }} = \frac{1}{{\sqrt {10} }}\) \(\tan B = \frac{{AC}}{{AB}} = \frac{{21}}{7} = 3\) \(\cot B = \frac{{AB}}{{AC}} = \frac{7}{{21}} = \frac{1}{3}\) Vì \(\angle B + \angle C = {90^0}\) \(\begin{array}{l} \Rightarrow \sin C = \cos B = \frac{1}{{\sqrt {10} }}\\\cos C = \sin B = \frac{3}{{\sqrt {10} }}\\\tan C = \cot B = \frac{1}{3}\\\cot C = \tan B = 3\end{array}\) Chọn A. Câu hỏi 11 : Cho tam giác \(ABC\) vuông tại \(A\), biết \(AB{\rm{ }} = {\rm{ 3}}cm,{\rm{ }}AC{\rm{ }} = 4cm.\) Giải tam giác \(ABC\).
Đáp án: D Phương pháp giải: Sử dụng định lý Pitago để tính cạnh BC. Sử dụng định nghĩa tỉ số lượng giác, tính chất hai góc phụ nhau. Từ tỉ số lượng giác suy ra số đo góc Lời giải chi tiết: Áp dụng định lý Pitago cho \(\Delta ABC\) vuông tại \(A\) có: \(A{B^2} + A{C^2} = B{C^2} \Leftrightarrow B{C^2} = {3^2} + {4^2} = 25 \Rightarrow BC = 5\) Xét \(\Delta ABC\) vuông tại \(A\) ta có: \(sinB = \frac{{AC}}{{BC}} = \frac{4}{5} \Rightarrow \angle B \approx {53^0}8'\) Vì \(\Delta ABC\) vuông tại \(A\) ta có: \(\angle B + \angle C = {90^0} \Leftrightarrow {53^0}8' + \angle C = {90^0} \Leftrightarrow \angle C \approx {36^0}52'\) Chọn D. Câu hỏi 12 : Trong hình vẽ bên, \(\sin C\) bằng
Đáp án: C Phương pháp giải: Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông: \(\sin = \dfrac{{doi}}{{huyen}}\). Lời giải chi tiết: Ta có: \(\sin C = \dfrac{{AB}}{{BC}}\). Chọn C. Câu hỏi 13 : Với góc nhọn \(\alpha \) tùy ý, khẳng định nào sau đây là Sai?
Đáp án: A Phương pháp giải: Sử dụng các công thức tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết: Ta có các công thức: \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }};\) \(\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }};\) \(\tan \alpha .\cot \alpha = 1;\) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1.\) Vậy chỉ có đáp án A sai. Chọn A. Câu hỏi 14 :
Đáp án: C Phương pháp giải: Lời giải chi tiết:
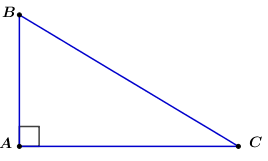
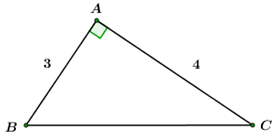
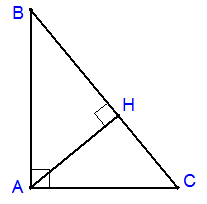
Câu hỏi 15 : Cho hình vẽ, chọn câu trả lời đúng:
Câu 3: Hệ thức đúng là:
Đáp án: B Phương pháp giải: Lời giải chi tiết: B Câu 4: Nếu tan B =
Đáp án: B Phương pháp giải: Lời giải chi tiết: B Câu hỏi 16 : Cho hình vẽ, chọn câu trả lời đúng:
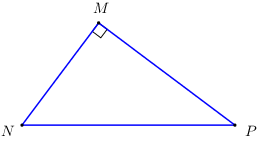
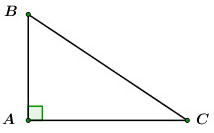
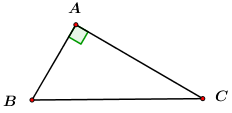
Câu 3: Hệ thức đúng là:
Đáp án: D Phương pháp giải: Lời giải chi tiết: D Câu hỏi 17 : Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3,AB = 4\). Khi đó \(\cos B\) bằng
Đáp án: D Phương pháp giải: - Áp dụng định lí Pi-ta-go để tìm độ dài cạnh \(BC\). - Sử dụng định nghĩa: \(cos\alpha \) = cạnh kề : cạnh huyền. Lời giải chi tiết: Tam giác \(ABC\) vuông tại \(A\), áp dụng định lí Pi-ta-go ta có: \(B{C^2} = A{B^2} + A{C^2} = {4^2} + {3^2} = 25 \Rightarrow BC = 5\) Khi đó \(\cos B = \frac{{AB}}{{BC}} = \frac{4}{5}\) Chọn D. Câu hỏi 18 : Cho tam giác \(MNP\) vuông tại \(M.\) Biết \(MN = 3cm,NP = 5cm.\) Tỉ số lượng giác nào đúng?
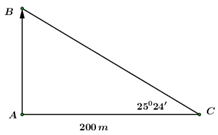
Đáp án: C Phương pháp giải: Áp dụng các tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết: Áp dụng định lí Pytago trong tam giác vuông MNP : \(MP = \sqrt {N{P^2} - M{N^2}} = \sqrt {{5^2} - {3^2}} = 4\,\,\left( {cm} \right)\). Ta có: \(\cot P = \frac{{MP}}{{MN}} = \frac{4}{3};\,\,\tan P = \frac{{MN}}{{MP}} = \frac{3}{4};\,\,\sin P = \frac{{MN}}{{NP}} = \frac{3}{5}\) Vậy đáp án đúng là C. Chọn C. Câu hỏi 19 : Tính chiều cao của đài kiểm soát không lưu Nội Bài. Biết bóng của đài kiểm soát được chiếu bởi ánh sáng mặt trời cuống đất dài \(200\,m\) và góc tạo bởi tia sáng với mặt đất là \({25^0}24'\) (kết quả làm tròn đến hàng đơn vị).
Đáp án: D Phương pháp giải: Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để làm bài. Lời giải chi tiết: Gọi các điểm như hình vẽ. Khi đó chiều cao của đài kiểm soát là: \(AB = AC.\tan \angle C = 200.\tan {25^0}24' \approx 95\,m.\) Chọn D. Câu hỏi 20 : Cho tam giác \(ABC\) vuông tại \(A\) như hình vẽ bên. Khẳng định nào dưới đây là đúng?
Đáp án: A Phương pháp giải: Tính cạnh huyền \(BC\) để sử dụng công thức \(\sin \) trong tam giác vuông \(ABC\): \(\sin B = \frac{{AC}}{{BC}}\) Lời giải chi tiết: Theo định lý Pytago: \(B{C^2} = A{C^2} + A{B^2} = {4^2} + {3^2} = {5^2} \Rightarrow BC = 5\) \( \Rightarrow \sin B = \frac{{AC}}{{AB}} = \frac{4}{5}\) Chọn A. Câu hỏi 21 : Cho tam giác vuông \(ABC\) vuông tại \(A\) thỏa mãn \(\cos B = \frac{3}{5}.\) Khẳng định nào dưới đây đúng?
Đáp án: A Phương pháp giải: Sử dụng các công thức liên hệ giữa các cạnh và tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết: Xét \(\Delta ABC\) vuông tại\(A\) ta có: \(\cos B = \frac{{AB}}{{BC}} = \frac{3}{5} \Rightarrow BC = \frac{5}{3}AB\) Chọn A. Câu hỏi 22 : Cho tam giác vuông \(ABC\) vuông tại \(A\) như hình vẽ bên. Khẳng định nào dưới đây đúng?
Đáp án: B Phương pháp giải: Sử dụng các công thức liên hệ giữa các cạnh và tỉ số lượng giác của góc nhọn trong tam giác vuông. Lời giải chi tiết: Xét \(\Delta ABC\) vuông tại\(A\) ta có: \(\begin{array}{l}B{C^2} = A{C^2} + A{B^2} \Leftrightarrow {10^2} = A{C^2} + {6^2} \Rightarrow AC = 8\\\cot B = \frac{{AB}}{{AC}} = \frac{6}{8} = \frac{3}{4}\end{array}\) Chọn B. Câu hỏi 23 : Tam giác \(ABC\) vuông tại \(A\) có \(AB = 3\,\,cm,\,\,AC = 4cm.\) Khi đó \(\cos C\)có giá trị bằng:
Đáp án: D Phương pháp giải: Áp dụng định lý Pytago trong tam giác \(ABC\) vuông tại \(A\): \(A{B^2} + A{C^2} = B{C^2}\) và \(\cos C = \frac{{AC}}{{BC}}.\) Lời giải chi tiết: Ta có: \(B{C^2} = A{B^2} + A{C^2} = {3^2} + {4^2} = 25 \Rightarrow BC = \sqrt {25} = 5\,\,\,\left( {cm} \right)\) \( \Rightarrow \cos C = \frac{{AC}}{{BC}} = \frac{4}{5}.\) Chọn D. Câu hỏi 24 : Cho tam giác \(ABC\) vuông tại \(A,\,\,\,BC = 4cm,\,\,\,AC = 2cm.\) Tính \(\sin \angle ABC.\)
Đáp án: B Phương pháp giải: Xét tam giác \(ABC\) vuông tại \(A\) ta có: \(\sin \angle ABC = \frac{{AC}}{{BC}}.\) Lời giải chi tiết: Xét tam giác \(ABC\) vuông tại \(A\) ta có: \(\sin \angle ABC = \frac{{AC}}{{BC}} = \frac{2}{4} = \frac{1}{2}.\) Chọn B. Câu hỏi 25 : Cho tam giác \(ABC\) vuông tại \(A,\,\,\angle ABC = {60^0},\) cạnh \(AB = 5cm.\) Độ dài cạnh \(AC\) là
Đáp án: C Phương pháp giải: Sử dụng công thức lượng giác trong tam giác vuông: \(AC = AB\tan B.\) Lời giải chi tiết: Xét tam giác \(ABC\) vuông tại \(A\) ta có: \(AC = AB\tan B = 5.\tan {60^0} = 5\sqrt 3 \,\,cm.\) Chọn C. Câu hỏi 26 : Tính các tỷ số lượng giác còn lại của \(\alpha \) biết: Câu 1: \(\sin \alpha = \frac{5}{{13}}\)
Đáp án: B Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\end{array} \right.\) Lời giải chi tiết: \(\sin \alpha = \frac{5}{{13}}\) Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1 \Leftrightarrow {\left( {\frac{5}{{13}}} \right)^2} + {\cos ^2}\alpha = 1\)\( \Leftrightarrow {\cos ^2}\alpha = 1 - \frac{{25}}{{169}} = \frac{{144}}{{169}}\)\( \Rightarrow \cos \alpha = \pm \frac{{12}}{{13}}\) Lại có: \({\tan ^2}\alpha + 1 = \frac{1}{{{{\cos }^2}\alpha }}\) \( \Leftrightarrow {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }} - 1 = \frac{{169}}{{144}} - 1 = \frac{{25}}{{144}}\) \( \Rightarrow \tan \alpha = \pm \frac{5}{{12}}\) \( \Rightarrow \cot \alpha = \frac{1}{{\tan \alpha }} = \pm \frac{{12}}{5}\) Chọn B. Câu 2: \(\tan \alpha = \frac{{12}}{{35}}\)
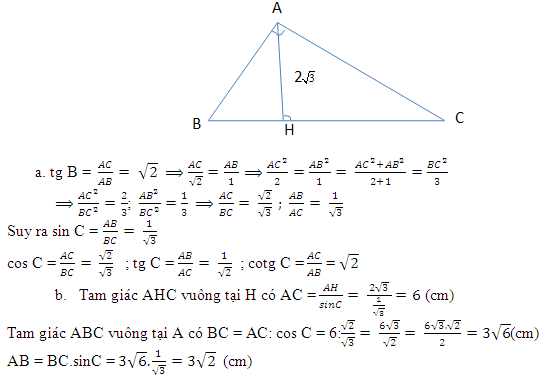
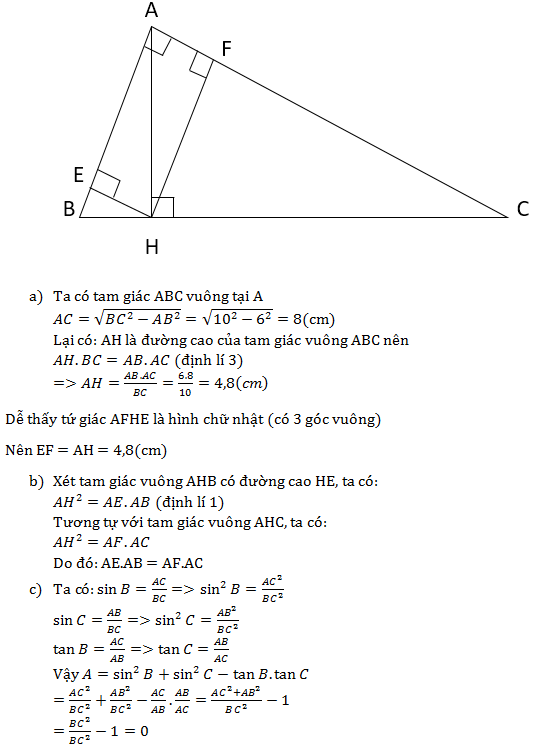
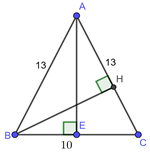
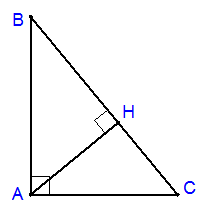
Đáp án: C Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\tan \alpha .\cot \alpha = 1\\1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\end{array} \right.\) Lời giải chi tiết: \(\tan \alpha = \frac{{12}}{{35}}\) Ta có: \(\tan \alpha .\cot \alpha = 1\)\( \Leftrightarrow \cot \alpha = \frac{1}{{\tan \alpha }} = 1:\frac{{12}}{{35}} = \frac{{35}}{{12}}\) Lại có: \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\)\( \Leftrightarrow 1 + {\left( {\frac{{12}}{{35}}} \right)^2} = \frac{1}{{{{\cos }^2}\alpha }}\)\( \Leftrightarrow \frac{1}{{{{\cos }^2}\alpha }} = \frac{{1369}}{{1225}}\)\( \Rightarrow {\cos ^2}\alpha = \frac{{1225}}{{1369}}\)\( \Rightarrow \cos \alpha = \pm \frac{{35}}{{37}}\) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)\( \Leftrightarrow {\left( {\frac{{35}}{{37}}} \right)^2} + {\sin ^2}\alpha = 1\)\( \Leftrightarrow {\sin ^2}\alpha = 1 - \frac{{1225}}{{1369}} = \frac{{144}}{{1369}}\)\( \Rightarrow \sin \alpha = \pm \frac{{12}}{{37}}\) Chọn C. Câu hỏi 27 : Cho \(\Delta ABC,\) đường cao \(AH\) và trung tuyến \(AM.\) Biết \(AH = 12cm;\,\,HB = 9cm;\,\,\,HC = 16cm.\) Tính tỷ số lượng giác của góc \(\angle HAM.\)
Đáp án: B Phương pháp giải: Lời giải chi tiết: Xét \(\Delta HAB\) và \(\Delta HCA\) ta có: \(\begin{array}{l} & \frac{{HB}}{{HA}} = \frac{9}{{12}} = \frac{3}{4}\\ & \frac{{HA}}{{HC}} = \frac{{12}}{{16}} = \frac{3}{4}\\ \Rightarrow \frac{{HB}}{{HA}} = \frac{{HA}}{{HC}} = \frac{3}{4}\end{array}\) Lại có \(\angle AHB = \angle AHC = {90^0}\)\( \Rightarrow HM = HC - MC = 16 - 12,5 = 3,5\,\,cm.\) \( \Rightarrow \left\{ \begin{array}{l}\angle BAH = \angle HCA\\\angle ABH = \angle HAC\end{array} \right.\) (các góc tương ứng). Mà \(\angle ABH + \angle BAH = {90^0} \Rightarrow \angle BAH + \angle HAC = {90^0}\) \( \Rightarrow \Delta ABC\) vuông tại \(A.\) Theo đề bài ta có \(AM\) là đường trung tuyến của \(\Delta ABC \Rightarrow AM = \frac{1}{2}BC = \frac{1}{2}\left( {HB + HC} \right) = \frac{1}{2}\left( {9 + 16} \right) = 12,5\,\,cm.\) Xét \(\Delta HAM\) vuông tại \(H\) ta có: \(\begin{array}{l}\sin \angle HAM = \frac{{HM}}{{AM}} = \frac{{3,5}}{{12,5}} = \frac{7}{{25}} & & & \cos \angle HAM = \frac{{AH}}{{AM}} = \frac{{12}}{{12,5}} = \frac{{24}}{{25}}\\\tan \angle HAM = \frac{{HM}}{{AH}} = \frac{{3,5}}{{12}} = \frac{7}{{24}} &&& \cot \angle HAM = \frac{{AH}}{{HM}} = \frac{{12}}{{3,5}} = \frac{{24}}{7}.\end{array}\) Câu hỏi 30 : Cho \(\Delta ABC\) vuông tại \(A\) có \(AB = 6cm,\,\,BC = 10cm,\) đường cao \(AH.\) Gọi \(E,\,\,F\) lần lượt là hình chiếu của \(H\) trên \(AB,\,\,AC.\) a) Tính \(EF.\) b) Chứng minh rằng \(AE.AB = AF.AC.\) c) Tính \(A = {\sin ^2}B + {\sin ^2}C - \tan B.\tan C.\)
Đáp án: A Phương pháp giải: Lời giải chi tiết:
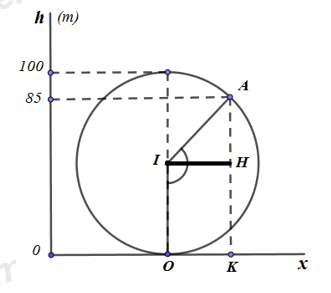
Câu hỏi 31 : Vòng quay mặt trời – Sun Wheel tại công viên Châu Á, Đà Nẵng có đường kính 100 m, quay hết một vòng trong khoảng thời gian 15 phút. Lúc bắt đầu quay, một người ở cabin thấp nhất (độ cao 0 m). Hỏi người đó đạt được độ cao 85m lần đầu tiên sau bao nhiêu giây (làm tròn đến 1/10 giây)?
Đáp án: A Phương pháp giải: Lời giải chi tiết:
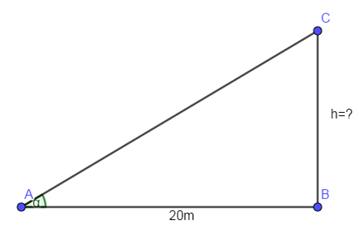
Vì độ cao 85m > 50m ( = R), nên ta có hình vẽ bên. \(\Delta AIH\)vuông tại H có: \(\sin \widehat{AIH}=\frac{AH}{IA}=\frac{AK-HK}{IA}=\frac{85-50}{50}=\frac{7}{10}\) \(\Rightarrow \widehat{AIH}\approx 44,{{42}^{0}}\Rightarrow \widehat{AIO}\approx 134,{{42}^{0}}\) Người đó đạt được độ cao 85m lần đầu sau số giây là: \(\frac{134,42}{360}.\left( 15.60 \right)\approx 336,1(s).\) Chọn: A. Câu hỏi 32 : Các tia sáng mặt trời tạo với mặt đất một góc xấp xỉ \({{30}^{o}}\) Tại thời điểm đó, bóng của một cái cây trên mặt đất dài \(20m\) Hỏi cái cây đó cao bao nhiêu mét ? (làm tròn tới phần thập phân thứ nhất).
Đáp án: C Phương pháp giải: Ta thừa nhận gốc cây đó mọc gần như vuông góc với mặt đất, từ đó sử dụng góc giữa tia nắng mặt trời với mặt đất để tính. Lời giải chi tiết: Ta có hình vẽ minh họa: Trong đó đoạn thẳng AB là độ dài của bóng cây, đoạn BC là chiều cao của cây Xét tam giác ABC vuông tại B có: \(\tan \alpha =\tan {{30}^{o}}=\frac{BC}{AB}=\frac{h}{20}\Rightarrow h=20.\tan {{30}^{o}}=11,5\left( m \right)\) Vậy chiều cao của cây là: \(h=11,5m\) Chọn C Câu hỏi 33 : Cho tam giác ABC vuông tại A. Biết rằng \(\frac{{AB}}{{AC}} = \sqrt 3 \). Số đo độ của góc ABC bằng:
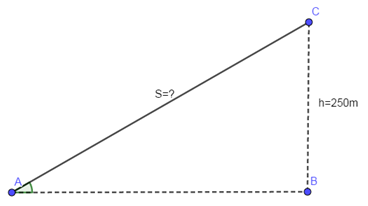
Đáp án: A Phương pháp giải: Sử dụng các công thức lượng giác để tìm số đo góc ABC. Lời giải chi tiết: Ta có: \(\cot ABC = \frac{{AB}}{{AC}} = \sqrt 3 \Rightarrow \angle ABC = {30^0}.\) Chọn A. Câu hỏi 34 : Một máy bay cất cánh theo phương có góc nâng là \({23^o}\)so với mặt đất. Hỏi muốn đạt độ cao 250m so với mặt đất thì máy bay phải bay lên một đoạn đường là bao nhiêu mét? (làm tròn đến mét)
Đáp án: A Phương pháp giải: Góc nâng của máy bay là góc tạo bởi hướng chuyển động bay lên của may bay với phương nằm ngang của mặt đất. Từ đó áp dụng công thức sin để tính đoạn đường mà máy bay cần bay để đạt độ cao 250m. Lời giải chi tiết: Ta có hình vẽ minh họa. Độ dài đoạn AC chính là quãng đường máy bay cần đi để đạt độ cao 250m. Xét tam giác ABC vuông tại B có: \(\sin \left( {\angle CAB} \right) = \frac{{BC}}{{AC}} \Rightarrow AC = \frac{{BC}}{{\sin \left( {\angle CAB} \right)}} = \frac{h}{{\sin {{23}^o}}} = \frac{{250}}{{\sin {{23}^o}}} \approx 640\left( m \right)\) Vậy máy bay cần bay quãng đường 640 (m) để đạt được độ cao 250 (m). Chọn A. Câu hỏi 35 : Cho tam giác vuông \(ABC\) vuông tại \(A\) như hình vẽ bên. Biết \(\cos B = \frac{5}{8};\) độ dài trung tuyến \(AM\) bằng
Đáp án: D Phương pháp giải: Tính cạnh huyền \(BC\) qua cos góc \(B\) sau đó sử dụng tính chất: Trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Lời giải chi tiết: Xét \(\Delta ABC\) vuông tại\(A\) ta có: \(\cos B = \frac{{AB}}{{BC}} = \frac{5}{{BC}} = \frac{5}{8} \Rightarrow BC = 8\) Do\(AM\) là trung tuyến của tam giác vuông \(ABC \Rightarrow AM = \frac{{BC}}{2} = \frac{8}{2} = 4.\) Chọn D. Câu hỏi 36 : Cho tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).
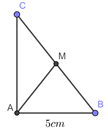
Đáp án: A Phương pháp giải: Sử dụng định nghĩa tỉ số lượng giác Tính chất tam giác cân. Công thức tính diện tích tam giác Lời giải chi tiết: Vì tam giác \(ABC\) cân tại\(A\) nên là \(AE\) đường cao đồng thời là đường trung tuyến \( \Rightarrow E\) là trung điểm \(BC \Rightarrow EB = EC = 5\) Xét \(\Delta ABE\)vuông tại \(E\) có: \(A{E^2} + E{B^2} = A{B^2}\) (Định lý Pi-ta-go) \(A{E^2} + {5^2} = {13^2} \Rightarrow AE = 12\) \( \Rightarrow {S_{ABC}} = \frac{{AE.BC}}{2} = \frac{{12.10}}{2} = 60\) Mặt khác: \({S_{ABC}} = \frac{{AC.BH}}{2} \Leftrightarrow 60 = \frac{{13.BH}}{2}\)\( \Rightarrow BH = \frac{{120}}{{13}}\) Xét \(\Delta ABH\)vuông tại \(H\) có: \(sinA = \frac{{BH}}{{BA}} = \frac{{120}}{{13}}:13 = \frac{{120}}{{169}}.\) Chọn A. Câu hỏi 37 : Tính diện tích hình bình hành \(ABCD\) biết \(AD = 12cm;DC = 15cm;\angle ADC = {70^0}\).
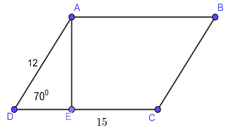
Đáp án: A Phương pháp giải: Sử dụng định nghĩa tỉ số lượng giác Công thức tính diện tích hình bình hành. Lời giải chi tiết: Xét \(\Delta ADE\) vuông tại \(E\) có: \(sinD = \frac{{AE}}{{AD}} \Leftrightarrow sin{70^0} = \frac{{AE}}{{12}} \Rightarrow AE = 12.sin{70^0}\) \( \Rightarrow {S_{ABCD}} = AE.DC = 12.\sin {70^0}.15 \approx 139,3\) Chọn A. Câu hỏi 38 : Cho tam giác \(ABC\) có góc \(B\) nhọn, các cạnh \(BC = a;AC = b;AB = c\). Chứng minh rằng: \({S_{ABC}} = \frac{1}{2}ac\sin B\). Phương pháp giải: Sử dụng định nghĩa tỉ số lượng giác. Công thức tính diện tích tam giác. Lời giải chi tiết: Xét \(\Delta ABH\)vuông tại \(H\) có: \(sinB = \frac{{AH}}{{AB}} \Leftrightarrow sinB = \frac{{AH}}{c} \Leftrightarrow AH = csinB\) \({S_{ABC}} = \frac{{AH.BC}}{2} = \frac{1}{2}ac\sin B\) (đpcm) Câu hỏi 39 : Chứng minh đẳng thức sau đúng với mọi \({0^0} < \alpha < {90^0}\) \(\frac{{{{\cot }^2}\alpha - {{\cos }^2}\alpha }}{{{{\cot }^2}\alpha }} + \frac{{\sin \alpha .cos\alpha }}{{\cot \alpha }} = 1\) Phương pháp giải: Sử dụng công thức lượng giác: \(\left\{ \begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\end{array} \right..\) Lời giải chi tiết: \(\begin{array}{l}VT = \frac{{{{\cot }^2}\alpha - {{\cos }^2}\alpha }}{{{{\cot }^2}\alpha }} + \frac{{\sin \alpha .cos\alpha }}{{\cot \alpha }}\\ = 1 - \frac{{{{\cos }^2}\alpha }}{{{{\cot }^2}\alpha }} + \frac{{\sin \alpha .cos\alpha }}{{\frac{{cos\alpha }}{{\sin \alpha }}}}\\ = 1 - \frac{{{{\cos }^2}\alpha }}{{\frac{{co{s^2}\alpha }}{{{{\sin }^2}\alpha }}}} + \frac{{\sin \alpha .cos\alpha }}{{\frac{{cos\alpha }}{{\sin \alpha }}}}\\ = 1 - {\sin ^2}\alpha + {\sin ^2}\alpha = 1 = VP\,\,\,\left( {dpcm} \right)\end{array}\) Câu hỏi 40 : Cho hai tam giác vuông \(OAB\) và \(OCD\) như hình vẽ. Biết \(OB = CD = a\), \(AB = OD = b.\) Tính \(\cos \angle AOC\) theo \(a\) và \(b\).
Đáp án: A Phương pháp giải: Tách \(\angle AOC = \angle AOB - \angle COD\). Áp dụng công thức cộng lượng giác và Pitago để tính \(\cos \angle AOC\) Lời giải chi tiết: Xét \(\Delta OAB\) và \(\Delta COD\) có: \(\begin{array}{l}\angle OBA = \angle CDO = {90^o}\,\,\,\,\left( {gt} \right)\\OB = CD\,\,\,\left( {gt} \right)\\AB = OD\,\,\,\,\left( {gt} \right)\\ \Rightarrow \Delta OAB = \Delta COD\,\,\,\left( {c - g - c} \right)\end{array}\) \( \Rightarrow OA = OC\) (2 cạnh tương ứng) \( \Rightarrow OA.OC = O{A^2} = O{B^2} + A{B^2} = {a^2} + {b^2}\) (Pitago) \(\begin{array}{l}\cos \angle AOC = \cos \left( {\angle AOB - \angle COD} \right) = \cos \angle AOB\cos \angle COD + \sin \angle AOB\sin \angle COD\\ = \frac{{OB}}{{OA}}.\frac{{OD}}{{OC}} + \frac{{AB}}{{OA}}.\frac{{CD}}{{OC}} = \frac{{OB.OD + AB.CD}}{{OA.OC}} = \frac{{ab + ab}}{{{a^2} + {b^2}}} = \frac{{2ab}}{{{a^2} + {b^2}}}.\end{array}\) Chọn A.
|















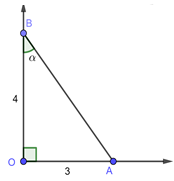
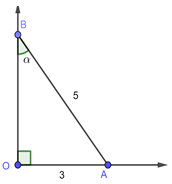

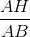
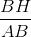
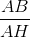
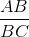
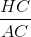
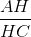
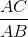
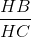
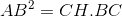
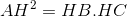
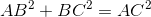
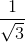 thì sin B =
thì sin B = 


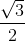
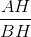
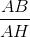
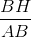
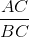
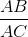
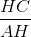
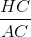
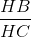
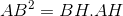
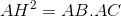
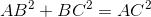
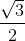 thì tanB =
thì tanB =