Nội dung từ Loigiaihay.Com
Câu hỏi:
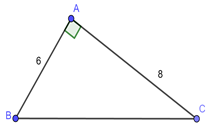
Cho hình vẽ. Tính tỉ số lượng giác của \(\angle B\) từ đó suy ra tỉ số lượng giác của \(\angle C\)
- A \(\begin{array}{l}\sin B = \frac{4}{5}\,\,;\,\,\cos B = \frac{3}{5}\,\,;\,\,\tan B = \frac{4}{3}\,\,;\,\,\cot B = \frac{3}{4}\\\sin C = \frac{3}{5}\,\,;\,\,\cos C = \frac{4}{5}\,\,;\,\,\tan C = \frac{3}{4}\,\,;\,\,\cot C = \frac{4}{3}\end{array}\)
- B \(\begin{array}{l}\sin B = \frac{3}{5}\,\,;\,\,\cos B = \frac{4}{5}\,\,;\,\,\tan B = \frac{3}{4}\,\,;\,\,\cot B = \frac{4}{3}\\\sin C = \frac{4}{5}\,\,;\,\,\cos C = \frac{3}{5}\,\,;\,\,\tan C = \frac{4}{3}\,\,;\,\,\cot C = \frac{3}{4}\end{array}\)
- C \(\begin{array}{l}\sin B = \frac{4}{5}\,\,;\,\,\cos B = \frac{3}{5}\,\,;\,\,\tan B = \frac{4}{3}\,\,;\,\,\cot B = \frac{3}{4}\\\sin C = \frac{4}{5}\,\,;\,\,\cos C = \frac{3}{5}\,\,;\,\,\tan C = \frac{4}{3}\,\,;\,\,\cot C = \frac{3}{4}\end{array}\)
- D \(\begin{array}{l}\sin B = \frac{3}{5}\,\,;\,\,\cos B = \frac{4}{5}\,\,;\,\,\tan B = \frac{3}{4}\,\,;\,\,\cot B = \frac{4}{3}\\\sin C = \frac{3}{5}\,\,;\,\,\cos C = \frac{4}{5}\,\,;\,\,\tan C = \frac{3}{4}\,\,;\,\,\cot C = \frac{4}{3}\end{array}\)
Phương pháp giải:
Sử dụng định lý Pi-ta-go.
Sử dụng định nghĩa tỉ số lượng giác, tính chất hai góc phụ nhau.
Lời giải chi tiết:
Xét \(\Delta ABC\) vuông tại \(A\) có : \(A{B^2} + A{C^2} = B{C^2}\) (Định lý Pi-ta-go)
\( \Leftrightarrow B{C^2} = {6^2} + {8^2} = 100 \Rightarrow BC = 10\,\,cm.\)
Trong \(\Delta ABC\) vuông tại \(A\) ta có:
\(\sin B = \frac{{AC}}{{BC}} = \frac{8}{{10}} = \frac{4}{5}\) \(\cos B = \frac{{AB}}{{BC}} = \frac{6}{{10}} = \frac{3}{5}\)
\(\tan B = \frac{{AC}}{{AB}} = \frac{8}{6} = \frac{4}{3}\) \(\cot B = \frac{{AB}}{{AC}} = \frac{6}{8} = \frac{3}{4}\)
Vì \(\angle B + \angle C = {90^0}\)
\( \Rightarrow \sin C = \cos B = \frac{3}{5}\) \(\cos C = \sin B = \frac{4}{5}\)
\(\tan C = \cot B = \frac{3}{4}\) \(\cot C = \tan B = \frac{4}{3}\)
Chọn A.