Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho hình lập phương ABCD.A’B’C’D’ có cạnh a. Khi đó \(\overrightarrow {AB} .\overrightarrow {A'C'} \) bằng ?
- A \({a^2}\sqrt 3 \).
- B \({a^2}\).
- C \(\dfrac{{{a^2}\sqrt 2 }}{2}\).
- D \({a^2}\sqrt 2 \).
Phương pháp giải:
Sử dụng công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\overrightarrow {\left| b \right|} .\cos \angle \left( {\overrightarrow a ;\overrightarrow b } \right)\).
Lời giải chi tiết:
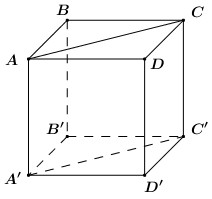
Vì \(\overrightarrow {AC} ;\,\,\overrightarrow {A'C'} \) là 2 vectơ cùng phương \( \Rightarrow \angle \left( {\overrightarrow {AB} ;\overrightarrow {A'C'} } \right) = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right) = \angle BAC = {45^0}\).
Do A’B’C’D’ là hình vuông cạnh a nên \(A'C' = a\sqrt 2 \).
Vậy \(\overrightarrow {AB} .\overrightarrow {A'C'} = AB.A'C'.\cos {45^0} = a.a\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = {a^2}\).
Chọn B.













