Phương pháp giải:

- Gọi N là trung điểm của BD. Chứng minh $MN \bot \left( {BCD} \right)$.

- Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó.

- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.

Lời giải chi tiết:

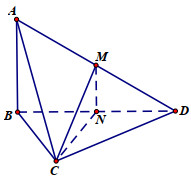
Gọi N là trung điểm của BD, ta có MN là đường trung bình của tam giác ABD nên MN // AB và $MN = \dfrac{1}{2}AB = a.$

Mà $AB \bot \left( {BCD} \right)\,\,\left( {gt} \right)$ nên $MN \bot \left( {BCD} \right)$, do đó CN là hình chiếu của CM lên (BCD)

$\Rightarrow \angle \left( {CM;\left( {BCD} \right)} \right) = \angle \left( {CM;CN} \right) = \angle MCN = \varphi$.

Vì tam giác BCD đều cạnh a nên $CN = \dfrac{{a\sqrt 3 }}{2}$.

Ta có: $MN \bot \left( {BCD} \right) \Rightarrow MN \bot CN$ $\Rightarrow \Delta CMN$ vuông tại N.

Vậy $\tan \varphi  = \tan \angle MCN = \dfrac{{MN}}{{CN}} = a:\dfrac{{a\sqrt 3 }}{2} = \dfrac{{2\sqrt 3 }}{3}$.

Chọn B.