Nội dung từ Loigiaihay.Com
Câu hỏi:
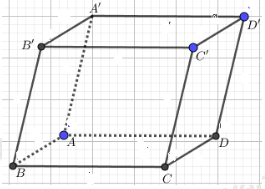
Cho hình hộp \(ABCD.A'B'C'D'\). Chọn khẳng định đúng ?
- A \(\overrightarrow {BA} ,\,\,\overrightarrow {BD} ,\,\,\overrightarrow {BD'} \) đồng phẳng.
- B \(\overrightarrow {BA} ,\,\,\overrightarrow {BC} ,\,\,\overrightarrow {B'D'} \) đồng phẳng.
- C \(\overrightarrow {BA'} ,\,\,\overrightarrow {BD'} ,\,\,\overrightarrow {BC'} \) đồng phẳng.
- D \(\overrightarrow {BD} ,\,\,\overrightarrow {BD'} ,\,\,\overrightarrow {BC} \) đồng phẳng.
Phương pháp giải:
Điều kiện 3 véctơ đồng phẳng:
- Cùng song song với một mặt phẳng.
- Tồn tại \(m,\,\,n\,\,\left( {{m^2} + {n^2} > 0} \right)\) sao cho \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b \).
Lời giải chi tiết:
Ta có \(ABCD\) là hình bình hành nên \(\overrightarrow {BD} = \overrightarrow {BA} + \overrightarrow {BC} \)
Mà \(\overrightarrow {BD} = \overrightarrow {B'D'} \)\( \Rightarrow \overrightarrow {B'D'} = \overrightarrow {BA} + \overrightarrow {BC} \) .
Vậy \(\overrightarrow {B'D'} ;\,\,\overrightarrow {BA} ;\,\,\overrightarrow {BC} \) đồng phẳng.
Chọn B.