Nội dung từ Loigiaihay.Com
Câu hỏi:
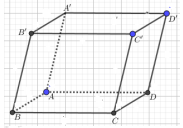
Cho hình hộp \(ABCD.A'B'C'D'\). Hệ thức nào đúng ?
- A \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} \).
- B \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AA'} \).
- C \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
- D \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AB'} \).
Phương pháp giải:
- Hình hộp có tất cả các mặt đều là hình bình hành.
- Sử dụng công thức ba điểm: \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {BC} \).
- Áp dụng công thức hình hành hành: Cho hình bình hành \(ABCD\), ta có: \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \).
Lời giải chi tiết:
Ta có: \(\overrightarrow {AC'} = \overrightarrow {AC} + \overrightarrow {CC'} \).
Vì \(ABCD\) là hình bình hành nên \(\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} .\)
Lại có: \(\overrightarrow {CC'} = \overrightarrow {AA'} \).
Do đó \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} .\)
Chọn C.