Nội dung từ Loigiaihay.Com
Câu hỏi:
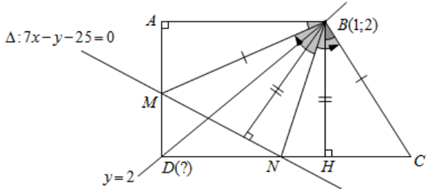
Trong mặt phẳng tọa độ \(Oxy,\) cho hình thang \(ABCD\) vuông tại \(A\) và \(D\), có \(AB = AD < CD\), điểm \(B\left( {1;2} \right)\), đường thẳng \(BD\) có phương trình \(y = 2\). Biết đường thẳng \(\Delta :7x - y - 25 = 0\) cắt các đoạn thẳng \(AD,\,\,CD\) lần lượt tại hai điểm \(M,\,\,N\) sao cho \(BM\) vuông góc với \(BC\) và tia \(BN\) là tia phân giác trong của \(\widehat {MBC}\). Biết điểm \(D\)biết có hoành độ dương, tọa độ điểm \(D\) là:
- A \(D\left( {2;\,\,5} \right)\)
- B \(D\left( { - 5;\,\, - 2} \right)\)
- C \(D\left( {5;\,\, - 2} \right)\)
- D \(D\left( {5;\,\,2} \right)\)
Phương pháp giải:
+ \(D \in BD:y = 2\) và điểm \(B\left( {1;2} \right)\)
+ \(BH = d\left( {B,\,\,CD} \right) = d\left( {B,\,\,\Delta } \right)\)
Lời giải chi tiết:
+) Gọi \(H\) là hình chiếu vuông góc của \(B\) trên \(CD\), khi đó \(ABHD\) là hình vuông.
Suy ra \(\angle CBH = \angle MBA\) (hai góc cùng phụ với \(\angle MBH\))
Từ đây ta có được \(\Delta CBH = \Delta MBA\) (g.c.g) \( \Rightarrow CB = MB \Rightarrow \Delta CBN = \Delta MBN\) (c.g.c)
Khi đó \(BH = d\left( {B,CN} \right) = d\left( {B,MN} \right) = \frac{{\left| {7 - 2 - 25} \right|}}{{\sqrt {50} }} = \frac{4}{{\sqrt 2 }} = 2\sqrt 2 .\)
Mà tam giác \(DHB\) vuông cân tại \(H\) nên \(BD = \sqrt 2 BH = 4\)
+) Gọi \(D\left( {t;2} \right) \in BD\) với \(t > 0\), khi đó: \(B{D^2} = 16 \Leftrightarrow {\left( {t - 1} \right)^2} = 16 \Leftrightarrow t = 5\) hoặc \(t = - 3\) (loại) \( \Rightarrow D\left( {5;2} \right)\)
Vậy \(D\left( {5;2} \right)\).
Chọn D.