Phương pháp giải:

+) \(AN \bot AM\) (t.c phân giác của hai góc kề bù) \(\Rightarrow\) đường tròn \(\left( C \right)\) sẽ có tâm \(I\left( { - 1;\,\, - 1} \right)\)  là trung điểm \(MN\), bán kính \(R = \frac{{MN}}{2} = \sqrt 5 \) \( \Rightarrow \left( C \right):{\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 5\)

+) Để  tìm tọa độ \(B,\,\,C\)  ta cần thiết lập phương trình đường thẳng \(BC\) rồi cho giao với đường tròn \(\left( C \right).\)

Lời giải chi tiết:

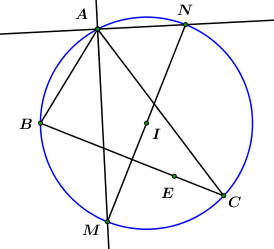
Ta có \(AM,\,\,AN\) là hai đường phân giác trong và ngoài của \(\angle A \Rightarrow AM \bot AN\) (tính chất các đường phân giác của một góc).

\( \Rightarrow \angle MAN = {90^0}\) \( \Rightarrow MN\) là đường kính của đường tròn \(\left( C \right)\) ngoại tiếp \(\Delta ABC.\)

\( \Rightarrow MN \bot BC.\)

Ta có: \(\overrightarrow {MN}  = \left( { - 2;\,\,4} \right) =  - 2\left( {1; - 2} \right).\)

Đường thẳng \(BC\) qua \(E\) và nhận \(\overrightarrow {MN} \) làm VTPT có phương trình: \(x - 2 - 2\left( {y + 1} \right) = 0 \Leftrightarrow x - 2y - 4 = 0.\)

Gọi \(I\) là trung điểm của \(MN \Rightarrow I\left( { - 1; - 1} \right)\)

Có: \(MN = \sqrt {{{\left( { - 2} \right)}^2} + {4^2}}  = 2\sqrt 5  \Rightarrow IM = \frac{1}{2}MN = \sqrt 5 .\)

Phương trình đường tròn \(\left( C \right)\) có tâm \(I\left( { - 1;\,\, - 1} \right)\) và đường kính \(MN\) là: \(\left( C \right):\,\,\,{\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 5.\)

Khi đó tọa độ các điểm \(B,\,\,C\) là nghiệm của hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}{\left( {x + 1} \right)^2} + {\left( {y + 1} \right)^2} = 5\\x - 2y - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2y + 4\\{\left( {2y + 5} \right)^2} + {\left( {y + 1} \right)^2} = 5\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 2y + 4\\5{y^2} + 22y + 21 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}y =  - \frac{7}{5}\\y =  - 3\end{array} \right.\\x = 2y + 4\end{array} \right. \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = \frac{6}{5}\\y =  - \frac{7}{5}\end{array} \right.\\\left\{ \begin{array}{l}x =  - 2\\y =  - 3\end{array} \right.\end{array} \right.\end{array}\)

Vì \(C\) có hoành độ dương \( \Rightarrow C\left( {\frac{6}{5}; - \frac{7}{5}} \right);\,\,\,B\left( { - 2; - 3} \right).\)

Chọn  D.