Phương pháp giải:

+) Áp dụng \(BG = 2GM\) để tìm tọa độ điểm \(M\) (\(M\) là trung điểm của \(AC\))

+) Gọi \(B'\) là điểm đối xứng của \(B\) qua phân giác góc \(A\) \( \Rightarrow B' \in AC\)

+) Phương trình cạnh \(AC\) đi qua \(M\) và \(B'\).

Lời giải chi tiết:

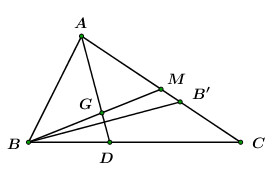
+) Gọi \(M\) là trung điểm của \(AC\), \(AD\) là phân giác trong góc \(A\) có phương trình: \(x - y - 1 = 0\)

+) Vì \(G\) là trọng tâm của \(\Delta ABC,\,\,BM\) là đường trung tuyến nên ta có: \(\overrightarrow {BG}  = 2\overrightarrow {GM} \)

\( \Rightarrow \left\{ \begin{array}{l}1 + 4 = 2\left( {{x_M} - 1} \right)\\1 - 1 = 2\left( {{y_M} - 1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = \frac{7}{2}\\{y_M} = 1\end{array} \right. \Rightarrow M\left( {\frac{7}{2};\,\,1} \right)\)

+) Phương trình đường thẳng \(d\) qua \(B\) và vuông góc với \(AD\)

 \( \Rightarrow \left( d \right):\,\,\,\,x + 4 + y - 1 = 0 \Leftrightarrow \,x + y + 3 = 0\)

Gọi \(I = \left( d \right) \cap AD\). Tọa độ điểm \(I\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}x - y - 1 = 0\\x + y + 3 = 0\end{array} \right. \Rightarrow I\left( { - 1;\,\, - 2} \right)\)

Gọi \(B'\) là điểm đối xứng của \(B\) qua phân giác góc \(A\) \( \Rightarrow B' \in AC\)

\( \Rightarrow \)\(I\) là trung điểm của \(BB'\)\( \Rightarrow B'\left( {2;\,\, - 5} \right)\)

Phương trình cạnh \(AC\) qua \(M\) và \(B'\) là:

\(AC:\,\,\,\frac{{x - 2}}{{\frac{7}{2} - 2}} = \frac{{y + 5}}{{1 + 5}} \Leftrightarrow 6\left( {x - 2} \right) = \frac{3}{2}\left( {y + 5} \right)\)\( \Leftrightarrow 4x - 8 = y + 5 \Leftrightarrow 4x - y - 13 = 0\)

Ta có: \(A = AC \cap AD\)\( \Rightarrow \) Tọa độ điểm \(A\) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}4x - y - 13 = 0\\x - y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 3\end{array} \right. \Rightarrow A\left( {4;\,\,3} \right)\)

Vậy \(A\left( {4;\,\,3} \right)\).

Chọn  A.