Nội dung từ Loigiaihay.Com
Câu hỏi:
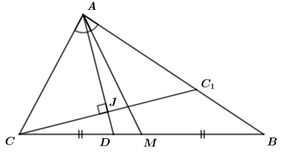
Trong mặt phẳng \(Oxy\), cho tam giác \(ABC\) biết \(C\left( {4;\,\,3} \right)\), đường phân giác \(AD\) và trung tuyến \(AM\) lần lượt có phương trình \(x + 2y - 5 = 0\) và \(4x + 13y - 10 = 0\). Phương trình đường thẳng \(AB\) là
- A \(x - 7y + 5 = 0\)
- B \(x + 7y + 5 = 0\)
- C \(7x + y - 25 = 0\)
- D \(7x + y + 25 = 0\)
Phương pháp giải:
+) Xác định tọa độ của điểm \(A\)
+) Gọi \(C'\) là điểm đối xứng của \(C\) qua phân giác \(AD\)\( \Rightarrow C' \in AB\)
+) Viết phương trình đường thẳng \(AB\) nhận \(\overrightarrow {AC'} \) là VTCP
Lời giải chi tiết:
+) Phương trình đường phân giác \(AD\): \(x + 2y - 5 = 0\)\( \Rightarrow {\vec n_{AD}} = \left( {1;\,\,2} \right),\,\,{\vec u_{AD}} = \left( {2;\,\, - 1} \right)\,\)
+) Phương trình đường trung tuyến \(AM:\,\,4x + 13y - 10 = 0\)
+) Vì \(A\) là giao điểm của \(AD\) và \(AM\) nên tọa độ điểm \(A\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x + 2y - 5 = 0\\4x + 13y - 10 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 9\\y = - 2\end{array} \right. \Rightarrow A\left( {9;\,\, - 2} \right)\)
+) Gọi \({C_1}\) là điểm đối xứng của \(C\) qua \(AD\)\( \Rightarrow {C_1} \in AB\)
Phương trình tổng quát của đường thẳng \(C{C_1}\) đi qua \(C\left( {4;\,\,3} \right)\) nhận \({\vec u_{AD}} = \left( {2;\,\, - 1} \right)\,\) là VTPT:
\(C{C_1}:\,\,\,2\left( {x - 4} \right) - \left( {y - 3} \right) = 0\)\( \Leftrightarrow 2x - 8 - y + 3 = 0\)\( \Leftrightarrow 2x - y - 5 = 0\)
+) Gọi \(J = C{C_1} \cap AD\).
Tọa độ của \(J\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}2x - y - 5 = 0\\x + 2y - 5 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 3\\y = 1\end{array} \right. \Rightarrow J\left( {3;\,\,1} \right)\)
\( \Rightarrow \) Tọa độ của điểm \({C_1}\) là: \(\left\{ \begin{array}{l}{x_{{C_1}}} = 2.3 - 4\\{y_{{C_1}}} = 2.1 - 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_{{C_1}}} = 2\\{y_{{C_1}}} = - 1\end{array} \right. \Rightarrow {C_1}\left( {2;\,\, - 1} \right)\)
+) \(\left. \begin{array}{l}A\left( {9;\,\, - 2} \right)\\{C_1}\left( {2;\,\, - 1} \right)\end{array} \right\} \Rightarrow \overrightarrow {A{C_1}} \left( { - 7;\,\,1} \right)\)
Phương trình đường thẳng \(AB\) đi qua \(A\left( {9;\,\, - 2} \right)\) và nhận \({\vec n_{A{C_1}}} = \left( {1;\,\,7} \right)\) là VTPT là:
\(AB:\,\,\,\,\,x - 9 + 7\,\left( {y + 2} \right) = 0\)\( \Leftrightarrow x - 9 + 7y + 14 = 0\)\( \Leftrightarrow x + 7y + 5 = 0\)
Vậy phương trình đường thẳng \(AB\) là: \(x + 7y + 5 = 0\)
Chọn B.