Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông tại \(A\)với \(AB = a;\)\(AC = 2a\). Mặt phẳng \(\left( {SBC} \right)\) vuông góc với mặt phẳng \(\left( {ABC} \right)\). Mặt phẳng \(\left( {SAB} \right)\); \(\left( {SAC} \right)\) cùng tạo với mặt phẳng \(\left( {ABC} \right)\) một góc bằng \(60^\circ \). Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SBC} \right)\). Tính tan\(\alpha \).
- A \(\dfrac{{\sqrt {51} }}{{17}}\)
- B \(\dfrac{{\sqrt {51} }}{3}\)
- C \(\dfrac{{\sqrt {17} }}{3}\)
- D \(\dfrac{{3\sqrt {17} }}{{17}}\)
Phương pháp giải:
Sử dụng công thức lượng giác trong tam giác.
Lời giải chi tiết:
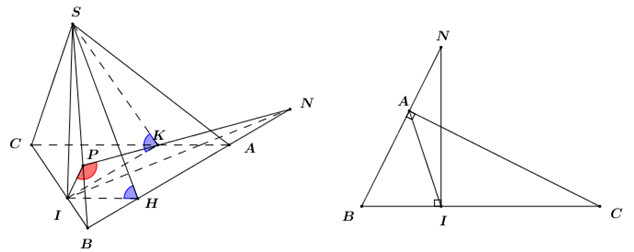
Trong \(\left( {SBC} \right)\), kẻ \(SI \bot BC\,\,\,\left( {I \in BC} \right)\) ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \bot \left( {ABC} \right)\\\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SI \bot BC\end{array} \right.\) \( \Rightarrow SI \bot \left( {ABC} \right)\)
Trong \(\left( {ABC} \right)\) kẻ \(IH \bot AB;\,\,\,IK \bot AC\,\,\left( {H \in AB,\,\,K \in AC} \right)\) ta có:
\(\left\{ \begin{array}{l}AB \bot IH\\AB \bot SI\,\,\left( {SI \bot \left( {ABC} \right)} \right)\end{array} \right. \Rightarrow AB \bot \left( {SIH} \right)\) \( \Rightarrow AB \bot SH\).
\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABC} \right) = AB\\\left( {SAB} \right) \supset SH \bot AB\\\left( {ABC} \right) \supset IH \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {ABC} \right)} \right) = \angle \left( {\left( {SH;IH} \right)} \right) = \angle SHI = {60^0}\).
Chứng minh tương tự ta có \(\angle SKI = {60^0}\).
Khi đó ta có: \(\Delta SIH = \Delta SIK\) (cạnh góc vuông – góc nhọn) \( \Rightarrow IH = IK \Rightarrow I\) là chân đường phân giác của góc \(A\). Áp dụng tính chất đường phân giác ta có: \(\dfrac{{IB}}{{IC}} = \dfrac{{AB}}{{AC}} = \dfrac{1}{2}\)\( \Rightarrow IB = \dfrac{1}{3}BC\).
Áp dụng định lí Pytago ta có: \(BC = \sqrt {A{B^2} + A{C^2}} = a\sqrt 5 \) \( \Rightarrow IB = \dfrac{{a\sqrt 5 }}{3},\,\,IC = \dfrac{{2a\sqrt 5 }}{3}\).
Trong \(\left( {ABC} \right)\) kẻ \(IN \bot BC\,\,\left( {N \in AB} \right)\).
Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \bot \left( {ABC} \right)\\\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {ABC} \right) \supset IN \bot BC\end{array} \right.\) \( \Rightarrow IN \bot \left( {SBC} \right)\) \( \Rightarrow IN \bot SB\).
Trong \(\left( {SBC} \right)\) kẻ \(IP \bot SB\,\,\left( {P \in SB} \right)\)
\( \Rightarrow SB \bot \left( {IPN} \right) \Rightarrow SB \bot NP\).
Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {SAB} \right) = SB\\\left( {SBC} \right) \supset IP \bot SB\\\left( {SAC} \right) \supset NP \bot SB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SBC} \right);\left( {SAB} \right)} \right) = \angle \left( {IP;NP} \right) = \angle IPN\).
Dễ thấy \(\Delta BNI \sim \Delta BCA\,\,\left( {g.g} \right)\) \( \Rightarrow \dfrac{{NI}}{{AC}} = \dfrac{{BI}}{{AB}} \Rightarrow NI = \dfrac{{2a.\dfrac{{a\sqrt 5 }}{3}}}{a} = \dfrac{{2a\sqrt 5 }}{3}\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{IH}}{{AC}} = \dfrac{{IB}}{{BC}} = \dfrac{1}{3} \Rightarrow IH = \dfrac{1}{3}AC = \dfrac{{2a}}{3}\).
Xét tam giác vuôn \(SHI\) có: \(SI = IH.\tan {60^0} = \dfrac{{2a}}{{\sqrt 3 }}\).
Áp dụng hệ thức lượng trong tam giác vuông \(SIB\) có: \(IP = \dfrac{{SI.IB}}{{\sqrt {S{I^2} + I{B^2}} }} = \dfrac{{2a\sqrt {15} }}{{3\sqrt {17} }}\).
Do \(IN \bot \left( {SBC} \right) \Rightarrow IN \bot IP\) nên \(\Delta INP\) vuông tại \(I\).
Vậy \(\tan \angle IPN = \dfrac{{IN}}{{IP}} = \dfrac{{\dfrac{{2a\sqrt 5 }}{3}}}{{\dfrac{{2a\sqrt {15} }}{{3\sqrt {17} }}}} = \dfrac{{\sqrt {51} }}{3} = \tan \alpha \).
Chọn B.













