Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho tứ diện ABCD có AB=a;AC=BC=AD=BD=a√32. Gọi M,N là trung điểm của AB,CD. Góc giữa hai mặt phẳng (ABD) ; (ABC) là α. Tính cosα biết mặt cầu đường kính MN tiếp xúc với cạnh AD.
- A 2−√3
- B 2√3−3
- C 3−2√3
- D √2−1
Phương pháp giải:
- Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Áp dụng định lí Cô-sin trong tam giác: cosA=b2+c2−a22bc.
Lời giải chi tiết:
Tam giác ABC,ABD là các tam giác cân tại C và D nên CM⊥AB,DM⊥AB.
Ta có: {(ABC)∩(ABD)=AB(ABC)⊃CM⊥AB(ABD)⊃DM⊥AB ⇒∠((ABC);(ABD))=∠(CM;DM)=α.
Gọi I là trung điểm của MN.
Kẻ IK⊥AD mà mặt cầu đường kính MN tiếp xúc với AD⇒IK=IM=IN.
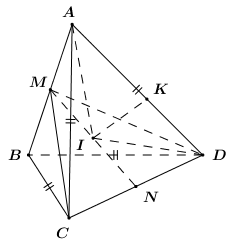
Xét ΔAMI và ΔAKI có:
∠AMI=∠AKI=900AIchungIM=IK(cmt)
⇒ΔAMI=ΔAKI (cạnh huyền – cạnh góc vuông).
⇒AM=AK=a2.
⇒DK=AD−AK=a√32−a2=a(√3−1)2.
Chứng minh tương tự ta có DK=DN⇒DN=a(√3−1)2 ⇒CD=a(√3−1).
Ta có: CM⊥AB nên ΔACM vuông tại M, áp dụng định lí Pytago ta có:
CM=√AC2−AM2=√3a24−a24=a√22.
Tương tự ta tính được DM=a√22.
Áp dụng định lí Cô-sin trong tam giác MCD có:
cos∠CMD=MC2+MD2−CD22.MC.MD=a22+a22−a2(√3−1)22.a22=2√3−3>0
Vậy cosα=cos∠CMD=2√3−3.
Chọn B.













