Câu hỏi trước
Nội dung từ Loigiaihay.Com
Câu hỏi:
Cho tứ diện \(ABCD\). Gọi \(M\) là trung điểm \(AB\) và \(G\) là trọng tâm \(\Delta BCD\). Đặt \(\overrightarrow {AB} = \overrightarrow b ,\,\,\overrightarrow {AC} = \overrightarrow c ,\,\,\overrightarrow {AD} = \overrightarrow d \). Hãy phân tích vectơ \(\overrightarrow {MG} \) theo \(\overrightarrow b ,\,\,\overrightarrow c ,\,\,\overrightarrow d \).
- A \(- \dfrac{1}{6}\left( {\overrightarrow b - 2\overrightarrow c - 2\overrightarrow d } \right)\)
- B \(\dfrac{1}{3}\left( {\overrightarrow a + 2\overrightarrow b - \dfrac{5}{6}\overrightarrow c } \right)\)
- C \(\dfrac{1}{2}\left( { - \overrightarrow a + \dfrac{4}{3}\overrightarrow b - \dfrac{1}{6}\overrightarrow c } \right)\)
- D \(\dfrac{1}{3}\overrightarrow a - \dfrac{1}{6}\overrightarrow b - \dfrac{5}{6}\overrightarrow c \)
Phương pháp giải:
Sử dụng công thức trọng tâm: Cho tam giác \(BCD\) có trọng tâm \(G\). Với mọi điểm \(M\) ta luôn có: \(\overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 3\overrightarrow {MG} \).
Lời giải chi tiết:
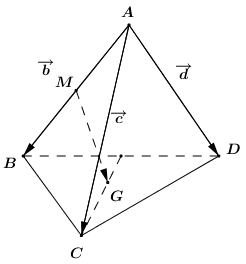
Vì \(G\) là trọng tâm tam giác \(BCD\) nên ta có:
\(\begin{array}{l}\,\,\,\,\,\,\overrightarrow {MG} = \dfrac{1}{3}\left( {\overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} } \right)\\ \Leftrightarrow \overrightarrow {MG} = \dfrac{1}{3}\left( {\dfrac{1}{2}\overrightarrow {AB} - \overrightarrow {CM} - \overrightarrow {DM} } \right)\\ \Leftrightarrow \overrightarrow {MG} = \dfrac{1}{6}\overrightarrow b - \dfrac{1}{3}.\dfrac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right) - \dfrac{1}{3}.\dfrac{1}{2}\left( {\overrightarrow {DA} + \overrightarrow {DB} } \right)\\ \Leftrightarrow \overrightarrow {MG} = \dfrac{1}{6}\overrightarrow b - \dfrac{1}{6}\left( {\overrightarrow {CA} + \overrightarrow {CA} + \overrightarrow {AB} } \right) - \dfrac{1}{6}\left( {\overrightarrow {DA} + \overrightarrow {DA} + \overrightarrow {AB} } \right)\\ \Leftrightarrow \overrightarrow {MG} = \dfrac{1}{6}\overrightarrow b - \dfrac{1}{6}\left( { - 2\overrightarrow c + \overrightarrow b } \right) - \dfrac{1}{6}\left( { - 2\overrightarrow d + \overrightarrow b } \right)\\ \Leftrightarrow \overrightarrow {MG} = \dfrac{1}{6}\overrightarrow b + \dfrac{1}{3}\overrightarrow c - \dfrac{1}{6}\overrightarrow b + \dfrac{1}{3}\overrightarrow d - \dfrac{1}{6}\overrightarrow b \\ \Leftrightarrow \overrightarrow {MG} = - \dfrac{1}{6}\overrightarrow b + \dfrac{1}{3}\overrightarrow c + \dfrac{1}{3}\overrightarrow d \\ \Leftrightarrow \overrightarrow {MG} = - \dfrac{1}{6}\left( {\overrightarrow b - 2\overrightarrow c - 2\overrightarrow d } \right)\end{array}\)
Vậy \(\overrightarrow {MG} = - \dfrac{1}{6}\left( {\overrightarrow b - 2\overrightarrow c - 2\overrightarrow d } \right)\).
Chọn A.