Nội dung từ Loigiaihay.Com
Câu hỏi:
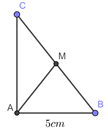
Cho tam giác vuông ABC vuông tại A như hình vẽ bên. Biết cosB=58; độ dài trung tuyến AM bằng
- A 5cm
- B 4,5cm
- C 3,5cm
- D 4cm
Phương pháp giải:
Tính cạnh huyền BC qua cos góc B sau đó sử dụng tính chất: Trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền.
Lời giải chi tiết:
Xét ΔABC vuông tạiA ta có:
cosB=ABBC=5BC=58⇒BC=8
DoAM là trung tuyến của tam giác vuông ABC⇒AM=BC2=82=4.
Chọn D.