Nội dung từ Loigiaihay.Com
Câu hỏi:
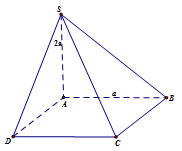
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình vuông cạnh \(a\). Đường thẳng \(SA\) vuông góc với mặt phẳng chứa đáy \(\left( {ABCD} \right)\), độ dài cạnh \(SA\) bằng \(2a\) (Tham khảo hình vẽ bên). Biết \(\overrightarrow {AC} = m\overrightarrow {AB} + n\overrightarrow {AD} + p\overrightarrow {AS} \). Tính tổng \(m + n + p\)
- A \(3.\)
- B \(2.\)
- C \(1.\)
- D \(0\)
Phương pháp giải:
Áp dụng quy tắc hình hình hành.
Lời giải chi tiết:
Ta có \(ABCD\) là hình vuông \( \Rightarrow \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \Rightarrow \left\{ \begin{array}{l}m = 1\\n = 1\\p = 0\end{array} \right. \Rightarrow m + n + p = 1 + 1 + 0 = 2\).
Chọn B.













