Nội dung từ Loigiaihay.Com
Câu hỏi:
Hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm \(O\). Hãy chỉ ra mệnh đề SAI?
- A \(\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \)
- B \(\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \)
- C \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \)
- D \(\overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow 0 \)
Phương pháp giải:
Sử dụng công thức: \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \,\,\forall M\), với \(I\) là trung điểm của \(AB\).
Lời giải chi tiết:
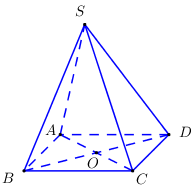
Do \(O\) là trung điểm của \(AC,\,\,BD \Rightarrow \left\{ \begin{array}{l}\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \\\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \end{array} \right. \Rightarrow \) Mệnh đề A, B đúng.
\( \Rightarrow \overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \Rightarrow \) Mệnh đề C đúng.
Chọn D













