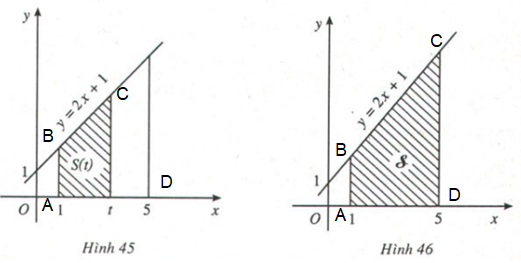
Trả lời câu hỏi 1 trang 101 SGK Giải tích 12

LG a

Tính diện tích $S$ của hình $T$ khi $t = 5$ (H.46).

Phương pháp giải:

Dựa vào công thức tính diện tích hình thang $ABCD (AB//CD)$ là:$S = \dfrac{{\left( {AB + CD} \right).h}}{2}$

Lời giải chi tiết:

(Hình 46)

Kí hiệu $A$ là điểm có tọa độ $(1,0), D$ là điểm có tọa độ $(5,0)$. $B, C$ lần lượt là giao điểm của đường thẳng $x = 1$ và $x = 5$ với đường thẳng $y = 2x + 1$.

- Khi đó $B$ và $C$ sẽ có tọa độ lần lượt là $(1,3)$ và $(5,11)$.

- Ta có: $AB = 3, CD = 11, AD = 4$. Diện tích hình thang:

$\displaystyle ABCD = {{(AB + CD).AD} \over 2} = 28$

Quảng cáo

LG b

Tính diện tích $S(t)$ của hình $T$ khi $x ∈ [1; 5]$.

Phương pháp giải:

Dựa vào công thức tính diện tích hình thang $ABCD (AB//CD)$ là:$S = \dfrac{{\left( {AB + CD} \right).h}}{2}$

Lời giải chi tiết:

Kí hiệu $A$ là điểm có tọa độ $(1,0)$, $D$ là điểm có tọa độ $(t,0)$. B, C\) lần lượt là giao điểm của đường thẳng $x = 1$ và $x = t$ với đường thẳng $y = 2x + 1$.

- Khi đó ta có $B (1,3)$ và $C(t, 2t + 1)$.

- Ta có $AB = 3, AD = t – 1, CD = 2t + 1$.

- Khi đó diện tích hình thang:

$\displaystyle S(t) = {{(AB + CD).AD} \over 2}$ $\displaystyle= {{(3 + 2t + 1).(t - 1)} \over 2}$ $= {t^2} + t - 2$

Do đó $S(t)= {t^2} + t - 2$

LG c

Chứng minh rằng $S(t)$ là một nguyên hàm của $f(t)=2t+1, t\in [1;5]$ và diện tích $S=S(5)-S(1)$.

Phương pháp giải:

Dựa vào công thức tính diện tích hình thang $ABCD (AB//CD)$ là:$S = \dfrac{{\left( {AB + CD} \right).h}}{2}$

Lời giải chi tiết:

Vì $S'(t)= ({t^2} + t - 2)'$ $=2t+1$ nên hàm số $S(t)$ là một nguyên hàm của hàm số $f(t)=2t+1, t\in [1;5]$.

Dễ thấy $S(5)-S(1)$ $=\left( {{5^2} + 5 - 2} \right) - \left( {{1^2} + 1 - 2} \right)$ $= 28 = S$ hay $S=S(5)-S(1)$.

HocTot.Nam.Name.Vn