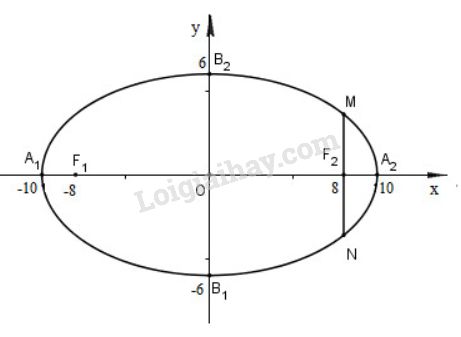
Bài 9 trang 99 SGK Hình học 10

LG a

Hãy xác định tọa độ các đỉnh, các tiêu điểm của elip $(E)$ và vẽ elip đó

Lời giải chi tiết:

Ta có: $a^2= 100 ⇒ a = 10$

$b^2= 36 ⇒ b = 6$

$c^2= a^2– b^2= 64 ⇒ c = 8$

Từ đó ta được:

+) Tọa độ các đỉnh: $A_1(-10; 0), A_2(10; 0), B_1(0; -3),$ $B_2(0;3)$

+) Tọa độ các tiêu điểm: $F_1(-8; 0), F_2(8; 0)$

LG b

Qua  tiêu điểm của elip dựng đường thẳng song song với $Oy$ và cắt elip tại hai điểm $M$ và $N$. Tính độ dài đoạn thẳng $MN$.

Lời giải chi tiết:

Gọi $d$ là đường thẳng đi qua $F_2(8;0)$ và song song $Oy$.

Khi đó $d:x=8$

$\begin{array}{l} M = d \cap \left( E \right)\\ \Rightarrow \left\{ \begin{array}{l} x = 8\\ \dfrac{{{x^2}}}{{100}} + \dfrac{{{y^2}}}{{36}} = 1 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} x = 8\\ \dfrac{{64}}{{100}} + \dfrac{{{y^2}}}{{36}} = 1 \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} x = 8\\ \dfrac{{{y^2}}}{{36}} = \dfrac{9}{{25}} \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} x = 8\\ {y^2} = \dfrac{{324}}{{25}} \end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l} x = 8\\ y = \pm \dfrac{{18}}{5} \end{array} \right. \end{array}$

Do đó có hai giao điểm của $d$ với $(E)$ là $M\left( {8;\dfrac{{18}}{5}} \right),N\left( {8; - \dfrac{{18}}{5}} \right)$

$MN = \sqrt {{{\left( {8 - 8} \right)}^2} + {{\left( { - \dfrac{{18}}{5} - \dfrac{{18}}{5}} \right)}^2}}$ $= \dfrac{{36}}{5}$

Cách khác:

Ta có: $M \in \left( E \right)$ $\Rightarrow M{F_1} + M{F_2} = 2a = 20\,\left( 1 \right)$

$MN//Oy \Rightarrow MN \bot {F_1}{F_2}$ $\Rightarrow \Delta M{F_2}{F_2}$ vuông tại ${F_2}$

Theo định lý Pitago ta có:

$\begin{array}{l}MF_1^2 - MF_2^2 = {F_1}F_2^2 = {\left( {2c} \right)^2} = {16^2}\\ \Rightarrow \left( {M{F_1} - M{F_2}} \right)\left( {M{F_1} + M{F_2}} \right) = {16^2}\end{array}$

Mà $M{F_1} + M{F_2} = 20$ nên

$\begin{array}{l}\left( {M{F_1} - M{F_2}} \right).20 = {16^2}\\ \Leftrightarrow M{F_1} - M{F_2} = \dfrac{{{{16}^2}}}{{20}} = \dfrac{{64}}{5}\,\left( 2 \right)\end{array}$

Từ (1) và (2) ta có hệ: $\left\{ \begin{array}{l}M{F_1} + M{F_2} = 20\\M{F_1} - M{F_2} = \dfrac{{64}}{5}\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}M{F_1} = \dfrac{{82}}{5}\\M{F_2} = \dfrac{{18}}{5}\end{array} \right.$

$\Rightarrow MN = 2M{F_2} = 2.\dfrac{{18}}{5} = \dfrac{{36}}{5}$

HocTot.Nam.Name.Vn