Bài 9 trang 64 SGK Hình học 10Tìm khẳng định sai trong các khẳng định sau đây: Đề bài Tìm khẳng định sai trong các khẳng định sau đây: A) \(\cos 35^0> \cos 10^0\) B) \(\sin 60^0 < \sin 80^0\) C) \(\tan 45^0< \tan 60^0\) D) \(\cos 45^0 = \sin 45^0\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết Nhận xét: Với hai góc α và β thỏa mãn 0º < α < β < 90º ta luôn có: cos α > cos β; sin α < sin β; tan α < tan β ; cot α > cot β Chú ý: Ta chứng minh nhận xét trên như sau:
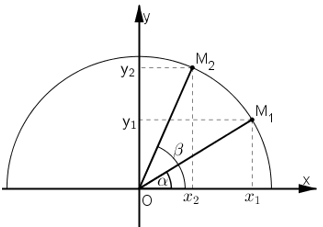
Biểu diễn góc α, β (α < β) trên nửa đường tròn lượng giác nằm phía trên trục hoành. Ta có sin α = y1; cos α = x1 ; sin β = y2; cos β = x2. + x1 > x2 nên cos α > cos β + y1 < y2 nên sin α < sin β. + \(\tan \alpha = \frac{{{y_1}}}{{{x_1}}},\tan \beta = \frac{{{y_2}}}{{{x_2}}}\) \(\begin{array}{l} \(\Rightarrow \frac{1}{{\cot \alpha }} < \frac{1}{{\cot \beta }} \Leftrightarrow \cot \alpha > \cot \beta \). Lời giải chi tiết Ta có: Vì \({35^0} > {10^0}\) nên cos 35º < cos 10º (A sai) Vì \({60^0} < {80^0}\) nên sin 60º < sin 80º (B đúng) Vì \({45^0} < {60^0}\) nên tan 45º < tan 60º (C đúng) Lại có: sin 45º = 1/ √2, cos 45º = 1/√2 nên sin 45º = cos 45º (D đúng). Chọn A. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
