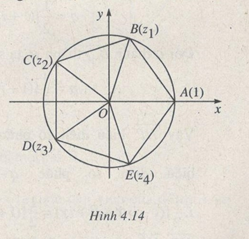
Câu 4.55 trang 184 sách bài tập Giải tích 12 Nâng cao

LG a

Chứng minh rằng $1,{z_1},{z_2},{z_3},{z_4}$ là các nghiệm của phương trình ${z^5} - 1 = 0$ và ${z_1} + {1 \over {{z_1}}} = 2\cos {{2\pi } \over 5}$

Giải chi tiết:

${z_1} = \cos {{2\pi } \over 5} + i\sin {{2\pi } \over 5},{z_2} = \cos {{4\pi } \over 5} + i\sin {{4\pi } \over 5}$

   ${z_3} = \cos {{6\pi } \over 5} + i\sin {{6\pi } \over 5},{z_4} = \cos {{8\pi } \over 5} + i\sin {{8\pi } \over 5}$

Từ đó theo công thức Moa-vrơ, $1,{z_1},{z_2},{z_3},{z_4}$ là nghiệm các phương trình ${z^5} - 1 = 0$ (đó là tất cả các nghiệm vì phương trình có bậc 5).

${z_1} + {1 \over {{z_1}}} = {z_1} + {\bar z_1} = 2\cos {{2\pi } \over 5}$

Quảng cáo

LG b

Viết ${z^5} - 1 = \left( {z - 1} \right)\left( {{z^4} + {z^3} + {z^2} + z + 1} \right)$ rồi đưa phương trình ${z^4} + {z^3} + {z^2} + z + 1 = 0$ về phương trình bậc hai đối với ẩn phụ ${\rm{w}} = z + {1 \over z}$. Từ đó suy ra $\cos {{2\pi } \over 5} = {{ - 1 + \sqrt 5 } \over 4}$

Giải chi tiết:

Với $z \ne 0,$

${z^4} + {z^3} + {z^2} + z + 1 = {z^2}\left( {{z^2} + {1 \over {{z^2}}} + z + {1 \over z} + 1} \right)$

$= {z^2}\left( {{{\left( {z + {1 \over z}} \right)}^2} + \left( {z + {1 \over z}} \right) - 1} \right)$

$= {z^2}\left( {{{\rm{w}}^2} + {\rm{w}} - 1} \right)$, trong đó ${\rm{w}} = z + {1 \over z}$

Phương trình ${{\rm{w}}^2} + {\rm{w}} - 1 = 0$ có hai nghiệm là ${{ - 1 \pm \sqrt 5 } \over 2}$

Vì ${z_1},{z_2},{z_3},{z_4}$ là bốn nghiệm của phương trình ${z^4} + {z^3} + {z^2} + z + 1 = 0$ tức là nghiệm của phương trình:

${\left( {z + {1 \over z}} \right)^2} + \left( {z + {1 \over z}} \right) - 1 = 0$ và ${z_4} = {\bar z_1} = {1 \over {{z_1}}},{z_3} = {\bar z_2} = {1 \over {{z_2}}}$  nên ${z_1} + {1 \over {{z_1}}},{z_2} + {1 \over {{z_2}}}$ là hai nghiệm phân biệt của phương trình ${{\rm{w}}^2} + {\rm{w}} - 1 = 0$

Từ đó suy ra $2\cos {{2\pi } \over 5} = {{ - 1 + \sqrt 5 } \over 2}$ (còn $2\cos {{4\pi } \over 5} = {{ - 1 - \sqrt 5 } \over 2}$) để ý rằng $\cos {{2\pi } \over 5} > 0,\cos {{4\pi } \over 5} < 0$ (h.4.14)

HocTot.Nam.Name.Vn