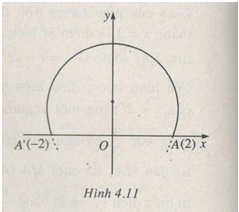
Câu 4.30 trang 182 sách bài tập Giải tích 12 Nâng cao

Đề bài

Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z sao cho ${{z - 2} \over {z + 2}}$ có một acgumen bằng ${\pi  \over 3}$

Quảng cáo

Lời giải chi tiết

${{z - 2} \over {z + 2}} = {{z\overline z - 4 + 2\left( {z - \overline z} \right)} \over {{{\left| {z + 2} \right|}^2}}}$ có một acgumen bằng ${\pi  \over 3}$ khi và chỉ khi $z\bar z - 4 + 2\left( {z - \bar z} \right) = l\left( {1 + i\sqrt 3 } \right)$, l là số thực dương.

Nếu viết $z = x + yi\left( {x,y \in R} \right)$ thì

 $\eqalign{& z\bar z - 4 + 2\left( {z - \bar z} \right) = {x^2} + {y^2} - 4 + 4yi \cr&\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\; = l + l\sqrt 3 i\left( { > 0} \right)  \cr&  \Leftrightarrow 4y = \left( {{x^2} + {y^2} - 4} \right)\sqrt 3  \cr&\Leftrightarrow {x^2} + {\left( {y - {2 \over {\sqrt 3 }}} \right)^2} - {{16} \over 3} = 0 \cr}$

Vậy M chạy trên cung tròn có tâm biểu diễn ${2 \over {\sqrt 3 }}i$ và có bán kính bằng ${4 \over {\sqrt 3 }}$ nằm ở phía trên trục thực.

Chú ý: A’, A là các điểm theo thứ tự biểu diễn -2. 2 thì điều kiện ${{z - 2} \over {z + 2}}$ có một acgumen bằng ${\pi  \over 3}$ có nghĩa là góc lượng giác tia đầu MA’, tia cuối MA’ (M là điểm biểu diễn z) bằng ${\pi  \over 3}$. Suy ra quỹ tích của M là cung tròn chứa góc ${\pi  \over 3}$ căng trên đoạn A’A (không kể A, A’) (h.4.11)

HocTot.Nam.Name.Vn