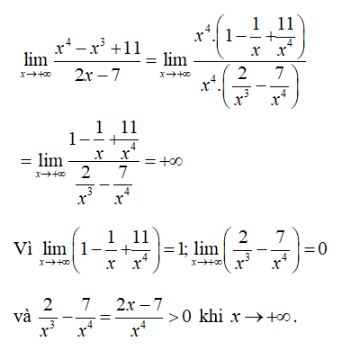Câu 42 trang 167 SGK Đại số và Giải tích 11 Nâng cao

LG a

\(\mathop {\lim }\limits_{x \to 0} \left( {{1 \over x} + {1 \over {{x^2}}}} \right)\)

Phương pháp giải:

Quy đồng mẫu thức tính giới hạn.

Lời giải chi tiết:

\(\mathop {\lim }\limits_{x \to 0} \left( {{1 \over x} + {1 \over {{x^2}}}} \right) = \mathop {\lim }\limits_{x \to 0} {{x + 1} \over {{x^2}}} = + \infty \)

vì  \(\mathop {\lim }\limits_{x \to 0} \left( {x + 1} \right) = 1 > 0,\) \(\mathop {\lim }\limits_{x \to 0} {x^2} = 0\,\text{ và }\,{x^2} > 0,\forall x \ne 0\)

LG b

\(\mathop {\lim }\limits_{x \to - 2} {{{x^3} + 8} \over {x + 2}}\)

Phương pháp giải:

Phân tích thành nhân tử, khử dạng vô định.

Lời giải chi tiết:

\(\eqalign{
& \mathop {\lim }\limits_{x \to - 2} {{{x^3} + 8} \over {x + 2}}\cr & = \mathop {\lim }\limits_{x \to - 2} {{\left( {x + 2} \right)\left( {{x^2} - 2x + 4} \right)} \over {x + 2}} \cr 
& = \mathop {\lim }\limits_{x \to - 2} \left( {{x^2} - 2x + 4} \right) = 12 \cr} \)

LG c

 \(\mathop {\lim }\limits_{x \to 9} {{3 - \sqrt x } \over {9 - x}}\)

Lời giải chi tiết:

\(\mathop {\lim }\limits_{x \to 9} {{3 - \sqrt x } \over {9 - x}}\) \( = \mathop {\lim }\limits_{x \to 9} \frac{{3 - \sqrt x }}{{\left( {3 - \sqrt x } \right)\left( {3 + \sqrt x } \right)}}\) \( = \mathop {\lim }\limits_{x \to 9} {1 \over {3 + \sqrt x }} = {1 \over 6}\)

LG d

\(\mathop {\lim }\limits_{x \to 0} {{2 - \sqrt {4 - x} } \over x}\)

Phương pháp giải:

Nhân cả tử và mẫu với biểu thức \(\left( {2 + \sqrt {4 - x} } \right)\).

Lời giải chi tiết:

\(\eqalign{
& \mathop {\lim }\limits_{x \to 0} {{2 - \sqrt {4 - x} } \over x} \cr & = \mathop {\lim }\limits_{x \to 0} \frac{{\left( {2 - \sqrt {4 - x} } \right)\left( {2 + \sqrt {4 - x} } \right)}}{{x\left( {2 + \sqrt {4 - x} } \right)}}\cr &= \mathop {\lim }\limits_{x \to 0} {{4 - \left( {4 - x} \right)} \over {x\left( {2 + \sqrt {4 - x} } \right)}} \cr 
&  = \mathop {\lim }\limits_{x \to 0} \frac{x}{{x\left( {2 + \sqrt {4 - x} } \right)}}\cr &= \mathop {\lim }\limits_{x \to 0} {1 \over {2 + \sqrt {4 - x} }} = {1 \over 4} \cr} \)

LG e

\(\mathop {\lim }\limits_{x \to + \infty } {{{x^4} - {x^3} + 11} \over {2x - 7}}\)

Lời giải chi tiết:

\(\mathop {\lim }\limits_{x \to + \infty } {{{x^4} - {x^3} + 11} \over {2x - 7}}\)

\( = \mathop {\lim }\limits_{x \to  + \infty } {x^3}\frac{{x - 1 + \frac{{11}}{{{x^3}}}}}{{x\left( {2 - \frac{7}{x}} \right)}} \) \(= \mathop {\lim }\limits_{x \to  + \infty } {x^3}.\frac{{1 - \frac{1}{x} + \frac{{11}}{{{x^4}}}}}{{2 - \frac{7}{x}}}=+\infty\)

Vì \(\mathop {\lim }\limits_{x \to  + \infty } {x^3} =  + \infty \) và \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{1 - \frac{1}{x} + \frac{{11}}{{{x^4}}}}}{{2 - \frac{7}{x}}} = \frac{1}{2} > 0\)

Cách khác:

LG f

 \(\mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^4} + 4} } \over {x + 4}}\)

Lời giải chi tiết:

 Với \(x < 0\), ta có :  \({{\sqrt {{x^4} + 4} } \over {x + 4}} = {{{x^2}\sqrt {1 + {4 \over {{x^4}}}} } \over {x + 4}} = x{{\sqrt {1 + {4 \over {{x^2}}}} } \over {1 + {4 \over x}}}\)

vì \(\mathop {\lim }\limits_{x \to - \infty } x = - \infty \) \(\text{ và }\) \( = \mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {1 + \frac{4}{{{x^2}}}} }}{{1 + \frac{4}{x}}} = 1 > 0\)

nên \(\mathop {\lim }\limits_{x \to - \infty } {{\sqrt {{x^4} + 4} } \over {x + 4}} = - \infty \)

HocTot.Nam.Name.Vn