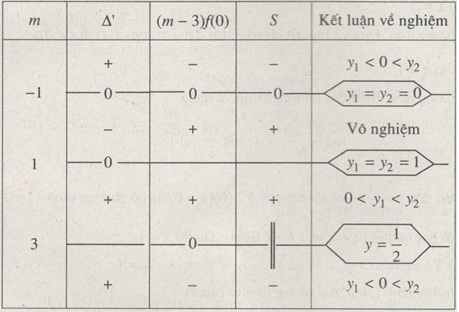
Câu 2.109 trang 88 sách bài tập Giải tích 12 Nâng caoTùy theo m ,hãy biện luận số nghiệm của phương trình: Đề bài Tùy theo m ,hãy biện luận số nghiệm của phương trình: \(\left( {m - 3} \right){.9^x} + 2\left( {m + 1} \right){.3^x} - m - 1 = 0\) Lời giải chi tiết Đặt \(y = {3^x}(y > 0)\), ta có \(\left( {m - 3} \right){y^2} + 2\left( {m + 1} \right)y - \left( {m + 1} \right) = 0\) (1) Số nghiệm của phương trình đã cho bằng số nghiệm dương của (1) - Xét \(m = 3\) thì (1) có nghiệm \(y = {1 \over 2}\) (thỏa mãn \(y > 0\)) - Nếu \(m \ne 3\) thì \(\Delta ' = {\left( {m + 1} \right)^2} + \left( {m + 1} \right)\left( {m - 3} \right) \) \(= 2\left( {m + 1} \right)\left( {m - 1} \right)\) Đặt \(f(y) = \left( {m - 3} \right){y^2} + 2\left( {m + 1} \right)y - \left( {m + 1} \right)\), ta có: \(\eqalign{& \left( {m - 3} \right)f(0) = \left( {3 - m} \right)\left( {m + 1} \right) \cr& S = {{2\left( {m + 1} \right)} \over {3 - m}} \cr} \) Lập bảng xét dấu: Từ bảng xét dấu ta có: - Với \(m\le - 1\) hoặc \(m \ge 3\) hoặc \(m = 1\) thì phương trình có một nghiệm, - Với \( - 1 < m < 1\) thì phương trình vô nghiệm. - Với \(1 < m < 3\) thì phương trình có hai nghiệm. HocTot.Nam.Name.Vn
|