Câu 20 trang 55 SGK Hình học 11 Nâng cao

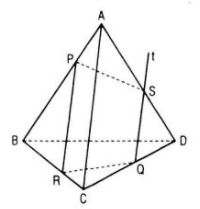
LG a

PR // AC

Phương pháp giải:

- Tìm giao tuyến của (PQR) với (ACD).

Sử dụng tính chất: Nếu hai mặt phẳng chứa hai đường thẳng song song thì chúng cắt nhau theo giao tuyến song song với đường thẳng đã cho.

- Tìm giao điểm S của AD với giao tuyến trên.

Lời giải chi tiết:

Trường hợp PR // AC

Ta có: \(\left\{ \begin{array}{l}
PR \subset \left( {PQR} \right)\\
AC \subset \left( {ACD} \right)\\
PR//AC\\
Q \in \left( {PQR} \right) \cap \left( {ACD} \right)
\end{array} \right. \) \(\Rightarrow \left( {PQR} \right) \cap \left( {ACD} \right) = Qt//AC\)

Trong (ACD), gọi S = Qt ∩ AD thì S = AD ∩ (PQR).

LG b

PR cắt AC

Lời giải chi tiết:

Trường hợp PR cắt AC

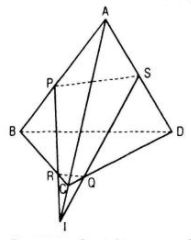
Trong (ABC), gọi I = PR ∩ AC

\( \Rightarrow \left\{ \begin{array}{l}
I \in AC \subset \left( {ACD} \right)\\
I \in PR \subset \left( {PQR} \right)
\end{array} \right.\)\( \Rightarrow I \in \left( {ACD} \right) \cap \left( {PQR} \right)\)

Mà \( Q\in \left( {ACD} \right) \cap \left( {PQR} \right)\)

⇒ (PQR) ∩ (ACD) = QI

Trong mp(ACD) ta có

S = QI ∩ AD thì S = AD ∩ (PQR).

HocTot.Nam.Name.Vn