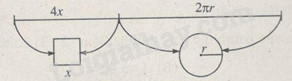
Bài 1.79 trang 26 SBT Giải tích 12 Nâng caoGiải bài 1.79 trang 26 sách bài tập Giải tích 12 Nâng cao. Một sợi dây kim loại dài 60cm được cắt thành hai đoạn. Đoạn dây thứ nhất được uốn thành hình vuông,đoạn dây thứ hai được uốn thành hình tròn ... Đề bài Một sợi dây kim loại dài 60cm được cắt thành hai đoạn. Đoạn dây thứ nhất được uốn thành hình vuông, đoạn dây thứ hai được uốn thành hình tròn. Phải cắt sợi dây như thế nào để tổng diện tích của hinh vuông và hinh tròn là nhỏ nhất ?
Lời giải chi tiết Gọi x là độ dài cạnh hình vuông và r là bán kính hình tròn. Độ dài cạnh hình vuông x=60π+4 (cm) Đoạn dây được uốn thành hình vuông có cạnh có độ dài là 240π+4≈33,6 (cm) Bán kính đường tròn r=30π+4 (cm) Đoạn dây được uốn thành vòng tròn có độ dài là 60ππ+4≈26,4 (cm) Ta có 4x+2πr=60 Từ x=12(30−πr),0<r<30π Tổng diện tích hình vuông và hình tròn là S=πr2+x2=πr2+14(30−πr)2 Dễ thấy S đạt giá trị nhỏ nhất tại điểm r=30π+4 HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
|
